Vor einigen Wochen habe ich in unserer Mathematik-Fachschaft in Cuenca eine Fortbildung zum Thema „Bruchrechnung“ gegeben. Auch hier in Ecuador ist der Einstieg in die Bruchrechnung Thema der 6.Klasse, ähnlich wie in Hamburg. Der Übergang von ganzen Zahlen zu Brüchen wird überwiegend recht abstrakt und wenig handlungsorientiert gestaltet, weshalb viele Schüler/innen auch in den folgenden Schuljahren Schwierigkeiten mit dem Thema haben. Ich habe einige Praxisbeispiele zusammengestellt und vorgestellt.
Ein Thema, das nach meinen Beobachtungen oft schwerfällt, ist die Unterscheidung zwischen Erweiterung und Mulitplikation von Brüchen, sowie wann ein gleichnahmiger Nenner benötigt wird und wann nicht. Auch in der achten Klasse begegnen mir Äußerungen, wie „Soll ich beim Multiplizieren nur oben oder auch unten malnehmen?“ oder „Muss ich die Brüche zum malnehmen auf den gleichen Nenner bringen, oder nicht?“ Und auch interessant: Ist es egal, in welcher Reihenfolge ich multipliziere? Warum ist es egal?
Ein zweites Thema ist die Ordnung von Brüchen. Es ist nicht sofort einsichtig, welcher Bruch größer ist, wenn zwei Brüche verglichen werden. Worauf muss ich achten, um Brüche zu ordnen?
Ein drittes Thema ist die Addition oder Subtraktion ungleichnahmiger Brüche. Warum muss ich auf den gleichen Nenner erweitern? Erweitere ich immer, indem ich den jeweils anderen Nenner verwende oder gibt es auch geschicktere Möglichkeiten?
Neben dem Arbeiten mit Material (Würfeln, verschieden langen und gefärbten Rechenstäbchen) habe ich meinen ecuadorianischen Kolleg/innen wärmstens Anschauungsbeispiele aus dem Buch „Mathematik als Abenteuer“ von Martin Kramer empfohlen und auf spanisch übersetzt. Hier geht es zum einen – etwas umfangreicher in der Vorbereitung – um das Mischen und Abfüllen von Flüssigkeiten in Bechern, um die Multiplikation von 3/4 mit 2/7 und die Kommutativität der Mulitiplikation einsichtig zu machen (Kommuntativität heißt, dass die Reihenfolge egal ist bei der Multiplikation, das Ergebnis bleibt gleich). Die andere, sehr einfach umzusetzende Darstellungsform des Autors ist das Arbeiten mit Flächen.
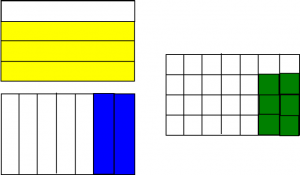
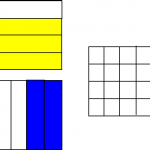
Zuerst teile ich eine Fläche in vier Teile vertikal und male drei davon aus. Danach teile ich eine weitere, gleich große Fläche horizontal in sieben Teile und male zwei davon aus. Die Multiplikation findet nun statt, indem die Schnittmenge beider farbigen Markierungen gezählt wird. Das sind in diesem Beispiel 3/4 von 2/7, also 6/28. Die Einteilung in 28tel geschieht über die vier vertikalen und sieben horizontalen Einteilungen. Ein schönes Verfahren, um auch die Kommutativität deutlich zu machen, denn wenn ich vertikale und horizontale Linien vertausche, ist die resultierende Fläche genauso groß.
Einen spielerischen Zugang zum Wiederholen, den ich mir überlegt habe, habe ich auch gleich einmal in meiner 8. und 10.Klasse ausprobiert. Ein bunter, vielseitiger Würfelkoffer und eine Zuordnung, welcher Würfel welche „Rolle“ in der Rechnung spielt und schon können Kleingruppen ihre eigenen Aufgaben würfeln.
von einem Kollegen ausgeliehen: Würfelkoffer, auch mit Rechenzeichen-Würfeln
„Rollenzuweisung“ an der Tafel
