Nun da das Schuljahr vorbei ist und die Ferien beginnen, finde ich zwischenzeitlich Zeit und Lust, noch ein paar Gedanken loszuwerden. Ich bin gerade in Ecuador, wo ich zwei Jahre als OLK in der Deutschen Schule in Cuenca gearbeitet hatte – ein erster Besuch seitdem wir wieder in Hamburg leben. Hier habe ich viele Impulse bekommen für sprachsensiblen Unterricht und viel über mich selbst gelernt in der Perspektive, „der Andere“ zu sein (was schwer zu vergleichen ist mit Migrant*innen in Deutschland, da ich hier im postkolonialen Ecuador viele Privillegien als „weißer“ europäischer Migrant hatte, also nicht von Rassismen betroffen bin, wie viele Menschen, die nach Deutschland und Europa kommen).
Ich möchte in diesem Artikel aber nicht über Ecuador oder das Unterrichten an Deutschen Auslandsschulen schreiben, sondern über sprachsensiblen Mathematikunterricht mit Geflüchteten in Hamburg.
Zunächst war meine Lerngruppe, so wie vermutlich viele der internationalen Vorbereitungsklassen (IVK) sehr heterogen in Lernstand, Vorbildung und Tempo, nicht allein fachlich, sondern auch in Bezug auf allgemeine Lernstrategien. Einige Jugendliche hatten vor ihrer Ankunft in Hamburg Mathe-Unterricht, andere seit Jahren nicht. Diese Umstände erfordern einen sehr individualisierten Unterricht, der aber in einer kleinen Lerngruppe, wie ich sie hatte – meist mit einer zusätzlichen pädagogischen Unterstützung – gut leistbar war. Die Klasse wird als 7.Klasse eingeordnet, das Niveau schwankt aber enorm.
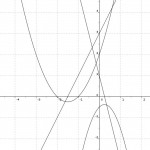
Die Themen bauen in der Mathematik nunmal stark aufeinander auf, so dass je nach Bedarf bei dem Rechnen mit Dezimalzahlen, wie in Klasse 7 durchaus üblich, angesetzt werden kann oder eben bei Bruchrechnung oder in einzelnen Fällen auch beim kleinen Einmaleins zurückgesprungen werden muss. Das alles ist kein Problem, da es keinen festen Lehrplan gibt, was so auch sinnvoll ist. Neben diesen eher auf Zahlenbereiche und Grundrechenarten bezogene Inhalte hat es sich angeboten, sowohl das Koordinatensystem und der Umgang mit dem Geodreieck einzubeziehen, als auch erste Erfahrungen mit digitalen Werkzeugen wie Geogebra anzubieten. Figuren zu zeichnen erfordert Konzentration und Feinmotorik und ist eine gute Abwechslung zum kalkülorientierten Hantieren mit Zahlen. Ein Koordinatensystem lässt sich auch prima mit Kreide auf dem Schulhof vorbereiten, um Schüler_innen dann Punkte oder Geraden aufstellen zu lassen. Messen und die Berechnung von Flächen und Volumina bieten einen guten Zugang zur direkten Umgebung und ermöglichen auch das Arbeiten im Freien und das Kennenlernen wichtiger Messgeräte wie Zollstock und Maßband. Eine Doppelstunde haben wir damit verbracht, verschiedene Strecken und Zeiten für einen 40 m Lauf zu messen und diese grafisch darzustellen, um die Darstellung von Daten zu üben und die Interpretation von Grafen, auch von Funktionen anzubahnen.
Ich bin in meinem ersten Durchgang relativ häufig thematisch gesprungen, es gab aber auch immer wieder Wechsel, d.h. Schüler_innen sind gegangen und gekommen, so dass ein „klassischer“ Aufbau kaum möglich war. Dies ist aber vielleicht auch eine Chance, den Unterricht stärker zu individualisieren und auf den/die Einzelne zuzuschneiden. Ich denke ein wichtiger Punkt ist neben individuellen Angeboten aber auch Kontinuität und Übung, d.h. viel selber rechnen, zeichnen, handeln. Es ist besonders schwierig, wenn zu hause wenig passiert und Materialien kaum strukturiert verwendet werden, was aber nicht überraschend ist, wenn man sich die Lebenssituation dieser jungen Menschen vor Augen hält. Diese sind geprägt von Unsicherheiten, wenig Struktur und wenig Kontinuität.
Die Fachsprache ist nicht nur für den fremdsprachlichen Fachunterricht eine eigene Herausforderung. Wie Objekte der Mathematik bezeichnet werden ist für die Verständigung wichtig, wichtiger aber erscheint mir noch das inhaltliche Verständnis. Ohne Begriffe wie „Multiplikation“ oder „Summe“ lässt es sich schwer arbeiten, aber ob es einen „Divisor“ gibt oder nicht, ist vielleicht weniger wichtig, als schriftlich multiplizieren und dividieren zu können. Wichtig bei der Einübung von Fachbegriffen erscheint mir das wiederholte Aufgreifen und Hervorheben einer überschaubaren Anzahl von zentralen Begriffen, ohne diese grammatikalisch einzuordnen. Einfache Sprache und Satzbildung (verbal und schriftlich als Tafelbild) ist manchmal gar nicht so einfach, lohnt sich aber sehr für das Verständnis.
Interessant waren hier die Vorkenntnisse einzelner Schüler_innen, die eine andere Schreibweise und Notation gelernt hatten, mit der sie aber ebenso wie mit meinem Vorschlag ans Ziel kommen. Hier habe ich mich bemüht, diese Vorkenntnisse zu stärken und wertzuschätzen und nicht die eine allgemeine Vorgehensweise durchzusetzen.
Ein Schuljahr ist eine kurze Zeit, um Grundlagen zu legen, aber ich denke alle Schüler_innen sind für sich einige Schritte vorangekommen. Manchmal habe ich vorhandenes Material genutzt, z.B. einzelne Seiten aus der „Intro“ Reihe, auch einmal Übungen aus unseren „RAAbits“-Ordnern die zu allen Arbeitsblättern Musterlösungen dabei haben, so dass auch recht eigenständiges Bearbeiten mit Musterlösung zum Vergleich möglich ist, d.h. auch, dass Schüler_innen zeitgleich einfach an unterschiedlichen Arbeitsblätter arbeiten können. Außerdem habe ich gelegentlich das Praxishandbuch „Sprachbildung im Mathematikunterricht“ verwendet. Viele Grafiken z.B. zur Bruchrechnung lassen sich aber leicht und ohne besondere Vorbereitung per Suchmaschine schnell im Netz finden und verwenden. Manchmal habe ich solche digitalen Grafiken auch abzeichnen lassen, das prägt sich auch besser ein, als diese als Kopie zu erhalten und spart Ressourcen.
Alles in allem gibt es viele Aspekte, die sich gar nicht so von anderem Mathe-Unterricht unterscheiden, vor allem das individuelle motivieren und verschiedene Zugänge und Niveaus einzuplanen. Ich freue mich auf das neue Schuljahr, wo ich voraussichtlich wieder etwas Mathematik-Unterricht in der IVK-Klasse geben werde und damit auch dazu beitragen kann, jungen Menschen in einer schwierigen Situation Wertschätzung und Bildungsangebote zu geben.

Notizen eines Schülers zu Fachbegriffen
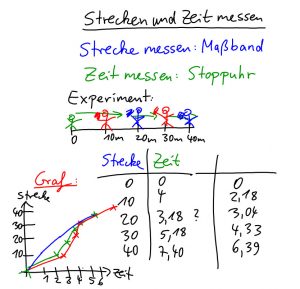
Ein Teil des Tafelbildes zum 40m Lauf
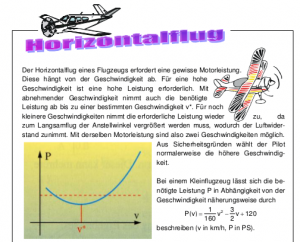
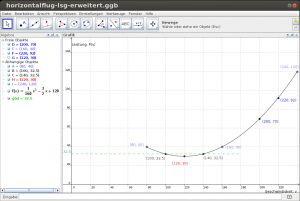
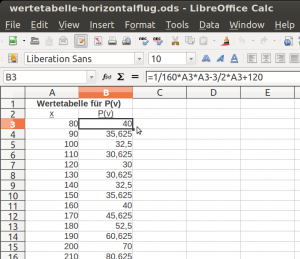
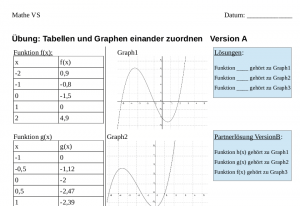
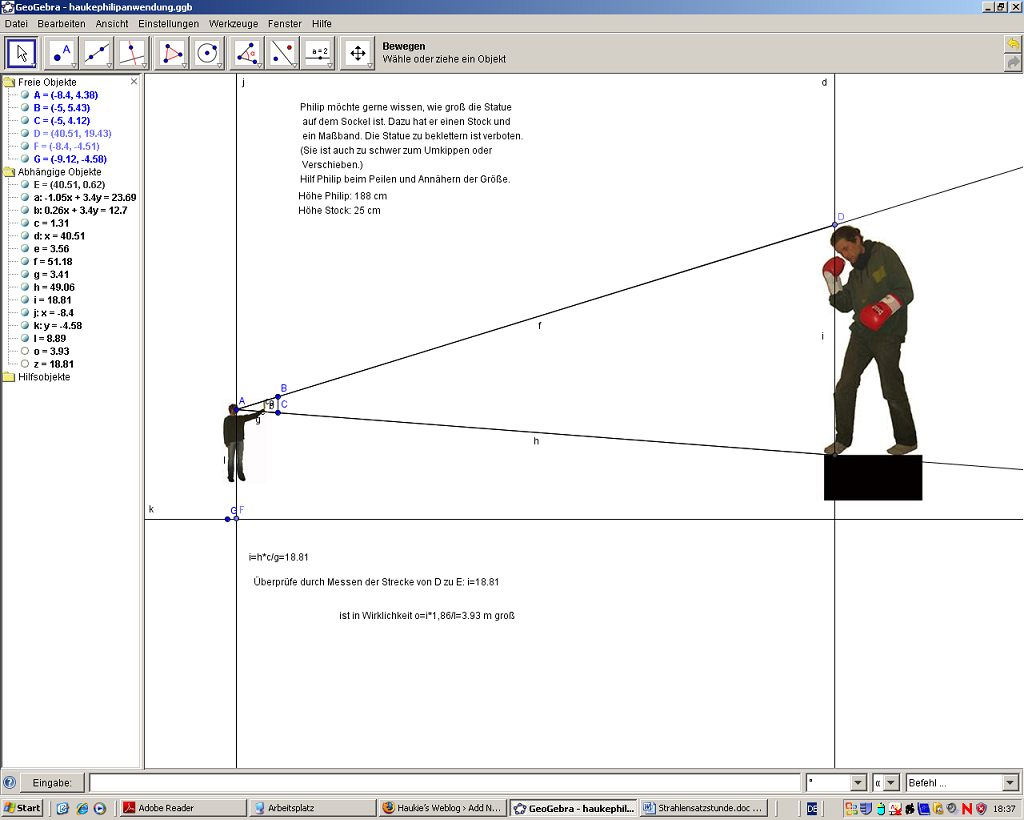
Ein Arbeitsblatt zu Geogebra: