Angeregt vom Buch Mathematik als Abenteuer von Martin Kramer habe ich in letzter Zeit in meiner 8.Klasse eimal einige Bewegungsspiele ausprobiert. Ich habe eine ermuedende Doppelstunde am Nachmittag, so dass Bewegung besonders angesagt ist. Continue reading »
Ab heute arbeiten wir im Mathe-Unterricht mit der offenen Plattform seacloud.cc. Thematisch steigen wir nun in die deskriptive Statistik ein. Aufmerksam geworden bin ich auf diese einfache und effektive Lösung zur digitalen „Materialverwaltung“ durch einen Kollegen an meiner Schule, der in seinem Fachunterricht in der gleichen Klasse ebenfalls Seacloud benutzt. Einfach zu handhaben, hier ein paar erste Eindrücke:
Jede Gruppe hat ihre Bibliotheken und Diskussionen
Als nöchstes probiere ich dann aus, digitale Arbeitsblattvorlagen zu verteilen und diese bearbeitet digital abgeben zu lassen
Diese Woche habe ich eine Hospitationsstunde in der 11.Klasse recht erfolgreich umgesetzt.
Gegenstand der Stunde war ein Text aus dem Bereich meiner Ausbildung. Hierzu hatte ich einleitend einige Folien zum Problemlösen mit Mathematik und zu meiner Ausbildungsstätte, dem DESY (Deutsches Elektronen Synchrotron) und dem Arbeiten an mechanischen Fertigungsmaschinen im Unterrichtsgespräch eingebracht. Leider kann ich die verwendeten Fotos aus Lizenzgründen nicht auf meinem Blog veröffentlichen, aber bei der Eingabe von DESY in Suchmaschinen lassen sich auch so viele interessante Bilder finden.
Anschließend an die Problematisierung verteilte ich Arbeitsblätter in die Kleingruppen und gab den Auftrag, eine Präsentationsfolie vorzubereiten. Dies hatte gegenüber dem Smartboard oder Postern den Vorteil, dass sie zügig beschriftet werden kann und in der Gruppe am Tisch direkt zur Verfügung steht. Es gibt doch immer wieder auch gute Gründe, nicht die modernste, sondern die passendste Technik einzusetzen.
Hier ist die Aufgabenstellung, die zentral für die Stunde war:
Planung der Produktion von Maschinenbauteilen
In einer Firma, die Maschinenteile herstellt gibt es eine Bandsäge, eine Fräsmaschine und eine Drehbank.
Die Bandsäge steht aus betriebsinternen Gründen 9000 Minuten pro Woche zur Verfügung,
die Fräsmaschine 5200 Minuten und die Drehbank 5100 Minuten.
Es sollen drei Maschinenteile hergestellt werden (eine Kegel, ein Flansch und eine Welle).
Der Kegel benötigt 2 Minuten an der Bandsäge, 4 Minuten an der Fräsmaschine und 7 Minuten an
der Drehbank je Stück. Der Flansch benötigt 8 Minuten an der Bandsäge, 6 Minuten an der
Fräsmaschine und keine Zeit an der Drehbank je Stück. Die Welle benötigt 6 Minuten an der
Bandsäge, 1 Minute an der Fräsmaschine und 2 Minuten an der Drehbank je Stück.
Aufgabe:
Berechne die Anzahl der Maschinenteile, die in einer Woche hergestellt werden können,
so dass alle drei Maschinen optimal ausgelastet sind.
Der Text war bewusst komplex gestaltet, um das Strukturieren und mathematisieren von Informationen zu fördern. Dies gelang insgesamt auch recht gut. Die Gelenkstelle zwischen Problematisierung und Erarbeitung hatte ich etwas ungeschickt gestaltet und den Austausch über die Ergebnisse konnte nur angerissen werden abe ansonsten war die Stunde sehr erfolgreich. Die Gruppen entwurfen verschiedene Modell und verwarfen sie teilweise wieder, wie es bei Modellierungsaufgaben typisch ist. Die Sicherung holte ich die anschließende Stunde nach, so dass das Thema abgerundet werden konnte. Besonders zur Sinnstiftung halte ich die Aufgabe für günstig, da Lineare Gleichungssysteme meinen Schüler/innen bisher eher als reines Kalkül begegnet sind und sich im Alltag kaum Anwendungen erschließen.
Spannend war auch, dass eine Gruppe auf eine sehr ungewöhnliche Lösung gekommen war, die auch solide Ergebnisse ergab: Sie gingen schrittweise vor, indem sie erst eine Maschine möglichst effektiv mit zwei Bauteilen auslasteten, um die übrig gebliebene Zeit mit dem dritten Bauteil aufzufüllen. Eine Probier-Methode, die die Einsicht ermöglichte, dass unterschiedliche Strategien zum Ziel führen können.
Hier ist das für die Veröffentlichung gekürzte Material inklusive Stundenentwurf: UE Planung Maschinenbau
In einer Fortbildung des Landesinstituts für Lehrerbildung in Hamburg zum Thema „interkulturelle Bildung“ haben wir uns an zwei Terminen mit verschiedenen Begriffen von „Kultur“ und Identitäten sowie der Sensibilisierung für einen transkulturellen Perspektivwechsel auseinandergesetzt.
Nach einer allgemeinen fachübergreifenden Einführung zu Identitäten und dem Umgang von Schule mit „Deutsch als Zweitsprache (DaZ)“ Schüler/innen beschäftigten wir uns handlungsorientiert mit Reaktionsmechanismen auf verschiedene „Regel“, um einen Umgang mit ungewohnten Verhaltensweisen durch eine sensibilisierte Sichtweise nachzuempfinden. Hierfür hatten wir ein Kartenspiel nach verschiedenen Regeln an verschiedenen Tischen gespielt ohne die Regeln explizit zu machen. Die Inhalte und Methoden bewegten den Blick weg vom „Problem mit den Schülern“ hin zum eigenen wertschätzenden Umgang mit „Fremdsein“ und dass nicht ohne Weiteres von sich auf andere geschlossen werden kann. Verschiedene Begrifflichkeiten und damit einhergehend Wertungen zu „Kultur“ wurden thematisiert und die Gespräche machten mir noch einmal deutlich, dass Erfahrungen mit „Fremdsein“ einigen Lehrer/innen durchaus fremd ist und wir als Lehrer/innen überwiegend weiß und bürgerlich mit Deutsch als erster Sprache behütet an Gymnasien sozialisiert wurden und somit systematisches Konfliktpotential in Schulen auftauchen muss. Dies einhergehend mit anderen gesellschaftlichen Rollen wie Gender, soziale Herkunft / Klasse und anderen Fremd- und Eigen-Identitätszuschreibungen erzeugt ein sehr komplexes Bild von sozialen Beziehungen in und um Schule.
Interessant fand ich bei der Beschäftigung mit den fachspezifischen didaktischen Überlegungen mit „transkultureller Brille“ (denn schließlich geht es weniger um Interkulturalität, also zwischen Kulturen arbeiten, sondern um die Einübung einer kulturübergreifenden und flexiblen Sichtweise auf kulturelle Praxen) die geringe Ausprägung dieser Sichtweise im Fach Mathematik. Sicherlich scheint Sprachunterricht zunächst naheliegender für eine transkulturelle Sichtweise zu sein, da Sprachförderung zur „Problembehebung“ mit DaZ Schüler/innen allgemein zum Standardprogramm gehört. Auf der anderen Seite erscheint gerade die Formalität und Fachsprache im Mathematik-Unterricht gerade für diese Schüler/inne mit DaZ eine Hürde darzustellen, die auf den Mangel an transkultureller Sichtweise in diesem Feld zurückzuführen ist. Wie in anderen Fächern auch gibt es eine doppelte Herausforderung für diese Schüler/innen, die Fachliche und die Sprachliche. Die Frage, die sich stellt, ist ob diesen Schüler/innen mit mehr Textarbeit und Sprachübungen im Mathematik-Unterricht geholfen ist oder mit bewusster Reduzierung der Fachsprache, um motivierende Erfolgserlebnisse zumindest auf mathematischer Ebenen zu ermöglichen. Ich denke wie häufig im pädagogischen Bereich gibt es nicht eine Antwort, sondern ein mehr oder weniger angemessenes Mischungsverhältnis. Insbesondere ist hierbei wichtig, die Unterrichtsvorbereitung und -nachbereitung immer wieder auch einmal durch eine „transkulturelle Brille“ zu reflektieren.
In unserer Kleingruppen-Arbeit zu Mathematik und transkultureller Bildung diskutierten wir eher über Zugänge zu mathematischen Konzepten allgemein, auch weil wir uns vorher in dieser Konstellation noch nie über didaktische Fragestellungen ausgetauscht hatten. Eines unserer Themen war: „Minus mal Minus gibt Plus“, wie kann das in den Horizont der Kinder gerückt werden? Ein weiteres Thema waren tragfähige Grundvorstellungen und Zugänge zu mathematischen Konzepten über verschiedene Strukturen wie grafische und ikonische Darstellungen und Arbeitsformen. Es wurde in Bezug auf andere Kulturkreise diskutiert, inwieweit Teamgeist und Kooperation in Kleingruppenarbeit stärker ausgeprägt seien und dies für den Unterricht nutzbar sei. Dann diskutierten wir über Aktivierung und Rollen in Gruppenarbeitsphasen sowie Anreize durch positive Verstärkung. Abschließend sprachen wir über Sprache und Mathematik-Unterricht. Mit einer transkulturellen Sichtweise kann in zwei Richtungen argumentiert werden, entweder die verstärkte Verwendung einfacher Sprache im Mathematikunterricht, um das Sprechen über Mathematik zu fördern und zu erleichtern oder entgegengesetzt die Verwendung von Sprache allgemein zu reduzieren, um die Doppelbelastung im Lernprozess zu reduzieren und auf die mathematischen Konzepte zu fokussieren. Viele Schüler/innen mit Deutsch als Zweitsprache haben Schwierigkeiten mit Formulierungen von Aufgaben. Dies lässt sich nach meiner Erfahrung im Sinne einer inklusiven Sichtweise noch weiter verschärfen darauf, dass allgemein auch Schüler/innen mit Deutsch als erster Sprache, die sprachliche Schwierigkeiten haben gleiche Doppelbelastungen erfahren.
In der Fachliteratur finden sich teilweise interessante Ansätze, die gerade die (mathematische) Sprachförderung ins Zentrum stellen, so beispielsweise das Arbeitsbuch „DaZ im Fachunterricht: Mathematik – Statistik für Anfänger“ (1). Auf der anderen Seite finden sich auch Aufgabentypen und inhaltliche Ansätze, die nach erster Sicht eher auf eigene Rassismen und Sensibilisierungen hinterfragt werden sollten. Wenn in Themenheften zu Mathematik und Interkulturalität neben „Tonleitern der Weltkulturen“ und „Kalenderberechnungen“ nur „Intelligenzvergleiche“, „Über- und Unterentwicklung“ und „Kriminalitätsraten“ als Titel auftauchen, darf man sich Sorgen machen, selbst wenn die Themen kritisch aufbereitet werden (was ich nur bedingt beurteilen kann, da ich sie nicht vollständig gesichtet habe, zudem ist einer der Artikel 11 Jahre alt). Da stellt sich die Frage, was für ein Bild von anderen Kulturen in Deutschland vorherrscht. Vergleiche (3) und (4)
Sinnvoll finde ich die folgende inhaltliche Bestimmungen auf der abstrakteren Ebene: „Im Mathematikunterricht kann die Vielfalt kultureller Wurzeln der eigenen Rechenkultur veranschaulicht, die Zahlensymbolik als Ausdruck bestimmter Weltdeutung behandelt oder bei Beispielaufgaben kulturelle Vielfalt repräsentiert werden.“ (http://www.bildungsserver.de/Mathematik-3383.html)
Das Buch „Zahlenwelten“ (2) hat ein ähnliches Mischungsverhältnis von Inhalten, die aus heutiger Sicht eher problematisch bis kontraproduktiv wirken, als auch Ansätze, die ich gerne ausprobieren möchte. Mathematisch logische Spiele aus anderen Kulturkreisen wie Patolli im Unterricht zu verwenden hat eben einen solchen wertschätzenden Bezug zu anderen Kulturen. Andererseits wird auch angeregt, statistisch „Ausländer an unserer Schule“ zu erheben und Berechnungen zu Unterkünften für Flüchtlinge anzustellen, die sicher kritisch begleitet Einsichten ermöglichen in gesellschaftliche Problemfelder, aber ebenso verstanden werden können, wie oben bereits benannt, dass andere Kulturen oder Kinder mit DaZ immer im negativen Kontext erwähnt werden oder als „das Andere“ dargestellt werden, statt ins Zentrum zu rücken, dass es kein „normal“ und „anders“ gibt, sondern alle Menschen in gewissen Kontexten als „normal“ gelten und in anderen als „anders“.
Zu unterscheiden bleibt das „strukturelle Mitdenken“ von transkultureller Bildung, z.B. durch Sprachwahl und Darstellungsarten und „inhaltliche Wandlung“ z.B. in Form vom wertschätzendem Aufgreifen verschiedener kulturell-historischer Wurzeln der Mathematik als Thema im Unterricht oder auch problemorientierte Beispiele, die nicht auf Fragestellungen aus dem Deutschen oder Europäischen Raum begrenzt bleiben.
Zum ersten Ansatz ist folgende Betrachtung hilfreich: „Betrachtet man das Spektrum schulischer Fächer genauer, so stellt sich heraus, dass es in allen Fächern kulturelle und fachgeschichtliche Prämissen und Traditionen gibt, die sich bei einer „interkulturellen Revision“ – mal mehr, mal weniger – als sperrig erweisen.“ (3) Beim zweiten Ansatz ist immer auch die Hinterfragung der eigenen Position als wohlmöglich Weißer Europäer mit Deutsch als Erstsprache unabdingbar, ist doch schnell aus gutem Vorhaben ein schräges Bild geworden, in dem es nicht um eine transkulturell reflektierte selbstbestimmte Identität der Schüler/innen, sondern um Zuschreibungen mit einhergehenden Wertungen von außen geht. Hier sollte nach meiner Einschätzung die Schüler/innen-Zentrierung in der Methodik besonders stark gemacht werden.
Literatur zum Thema:
(1) Nina Bödeker Olaf Gent: „DaZ im Fachunterricht: Mathematik – Statistik für Anfänger“ 5./6. Klasse, Persen Verlag 2010 (http://buecher-de.welt.de/shop/deutsch-als-fremdsprache/mathematik-statistik-fuer-anfaenger/boedeker-nina-gent-olaf/products_products/detail/prod_id/30530497/)
(2) Joachim Schroeder: „Zahlen-Welten: Bausteine für einen interkulturellen Mathematikunterricht“ Armin Vaas Verlag, 1994 (http://www.buchpreis-suche.de/zahlen-welten-bausteine-f%C3%BCr-einen-interkulturellen-mathematikunterricht.htm)
(3) Mathematik-Unterrichts-Einheiten-Datei e.V. „interkulturelles Lernen„: http://www.mued.de/html/inhalte/i3-multikulti.html
(4) Handreichung: Impulse für das interkulturelle Lernen Forum 1 / 2001, UNESCO Projekt Schulen http://www.ups-schulen.de/forum/01-1/forum-27-37.pdf
(5) S.Prediger: „Mathematiklernen als interkulturelles Lernen – Entwurf für einen didaktischen Ansatz„, in: Journal für Mathematikdidaktik 22 (2001) (http://www.mathematik.uni-dortmund.de/~prediger/veroeff/01-jmd-ml-as-ik.html)
Ich würde gerade gerne mehr schreiben, aber da vieles Material, was ich im Unterricht verwende nicht ausschließlich von mir erstellt ist (was ich auch nicht als primäre Aufgabe von Lehrer/innen sehe) sondern Kompositionen darstellt, kann ich gar nicht so viel publizieren, wie ich gerne würde.
Aber gelegentlich werde ich dies selbstverständlich weiterhin tun.
Gutes Material empfehlen kann ich allerdings:
Für meinen Informatik-Unterricht, beispielsweise den Kurs zu Objektorientierter Programmierung, verwende ich häufig die Materialien von meinem Kollegen Uwe Debacher: www.debacher.de der sein Material ebenfalls unter Creative Commons zur Verfügung stellt und viel mit Wiki-Tutorials arbeitet.
Für Lego Mindstorms benutze ich gelgentlich ein Lehrerhandbuch, welches unters traditionelle Copyright fällt und zu kaufen ist und hier dementsprechend nicht veröffentlicht wird. Zudem hat Uwe Debacher auch hier einiges veröffentlicht und ich habe auch eigenes Material bereits auf diesen Blog gestellt, das ich wiederverwende und weiterentwickle. Viele Aufgaben sind in diesem Bereich projektförmig und lassen sich mit den Schüler/innen auch gut gemeinsam in Ideensammlungen ohne zusätzliches Material entwickeln.
Für den Mathematik-Unterricht in der Vorstufe verwende ich teilweise das Arbeitsheft von Klett „Zum Übergang von der Realschule in die Oberstufe„, das ich auf einer Fachtagung zur Brückenfunktion der Vorstufe in den Hamburger Stadtteilschulen zufällig in die Hände bekam, kaufte und sehr angetan war von dem Aufbau als Selbstlern-Heft mit Selbsttests und Übungsaufgaben zu moderner Mathematik, also auch viel Problemlöse- und Modellierungsaufgaben. In der Schule nutzen wir das Buch „Elemente der Mathematik„, welches ich gerne und gut nutze, allerdings fehlen mir auch noch die Konkurrenz-Vergleiche anderer Mathematik-Schulbücher. Inspirierende für die Mathematik finde ich auch immer wieder die online verfügbaren Aufgaben der Hamburger Behörde zu den zentralen schriftlichen Überprüfungen.
Soweit erstmal zum Unterrichten und den Lizenzen. Fortsetzung folgt…
In den letzten Wochen habe ich in meinem Vorstufen-Kurs mehrmals die dynamische Geometriesoftware Geogebra eingesetzt.
Zum einen für Demonstrationen vorne am Smartboard, zum anderen zur eigenständigen Bearbeitung von dynamischen Arbeitsblättern und schlussendlich auch zur Erzeugung von Grafiken per Screenshot für Papierarbeitsblätter und eine Klassenarbeit.
Zur Demonstration des grafischen Ableitens habe ich ein bereits verfügbares dynamisches Material verwendet, das die Tangentensteigung als Spur markiert:
http://www.geogebratube.org/material/show/id/1291
Hier habe ich ein eigenes Arbeitsblatt entwickelt, dass die Möglichkeiten von Geogebra allerdings bei weitem nicht ausschöpft:
http://www.geogebratube.org/material/show/id/6972
Und hier ist einer der Screenshots mit dazugehörigem Arbeitsblatt:
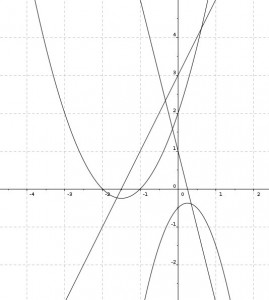Arbeitsblatt (OpenOffice Datei)
Arbeitsblatt (pdf Datei)
Und die Aufgabe aus der Klausur (wobei ich die Skalierung ungeschickt gewählt hatte, da hätte ich besser von -7 bis +7 als y Bereich wählen sollen:
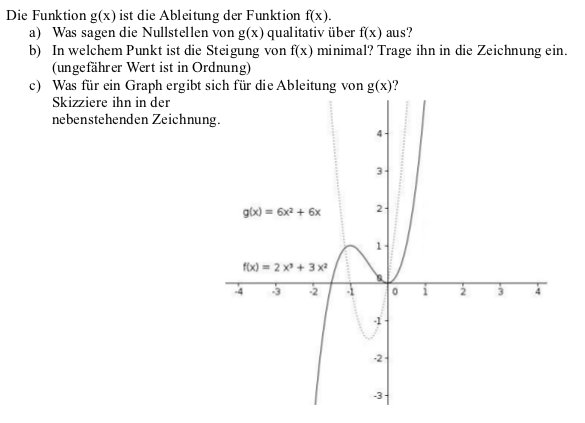Insgesamt ist das Arbeiten mit Geogebra vor allem für dynamische Zusammenhänge sehr nützlich und sowohl für Präsentationen von Konzepten als auch zur selbstständigen Bearbeitung sehr hilfreich. Zur Erarbeitung didaktisch passender dynamischer Materialien braucht es etwas Zeit, aber es gibt auch schon eine ganze Reihe frei verfügbarer Materialien, die in ein Unterrichtsvorhaben eingebettet werden können.
Zum anstehenden Thema Kurvendiskussion in meinem Kurs werde ich beispielsweise sicher auf das Material Differentialrechnung – Wendepunkte – Sachsenringkurve verwenden.
Heute findet die i-learn Tagung am LI in Hamburg statt. Es gibt auch einen Twitter-Hashtag: #ilearnhh
Im ersten Workshop von Torsten Otto beschäftigten wir uns mit dem Konzept des „Flipped Classroom“ / „Umgedrehter Unterricht„. Nach einigen Beispielen aus der Mathematik auf youtube, den „Mathesongs“ aus Schülersicht betrachteten wir verschiedene Tools, u.a. Jing für Windows und Exlain Everything fürs I-Pad und erstellten eigene kleine Produkte mit diesen Werkzeugen.
Abschließend haben wir uns einige Ergebnisse angeschaut, u.a. ein gehörlosen-Video zum Thema „Aufbau des Auges“, eine Webcam-Aufnahme zum Satz des Pythagoras und ein kleiner Clip zur Flächenberechnung eines Dreiecks von mir. Ich habe keinen Youtube-Account und konnte den mit Explain Everything erstellten Clip nicht online bekommen. Aber so besonders toll war das erste Ergebnis auch noch nicht. Demnächst hoffendlich mehr 🙂
Erfahrungswert war vor allem, dass man sich vorher (noch) genauer überlegen sollte, was man sagen will.
Im Nachmittagsteil war ich im Workshop „Stationenlernen 2.0“ von Thomas Kubitza, der verschiedene mathematische und physikalische Stationen vorbereitet hatte, die wir ausprobieren und auswerten konnten.
Verwendete Software, die besonders für meinen Matheunterricht interessant sein könnte ist „Quick Graph„, das sowohl 2D als auch 3D Funktionen als Grafik rendert und das mir bereits bekannte „Bettermarks„. Aber auch das Simulationsprogramm Algodoo, mit dem wir physikalische Experimente zu Reibung und Lichtbrechung durchführten könnte als Ergänzung in der technischen Informatik nützlich sein. Leider handelt es sich nicht um Open-Source Projekte, aber gerade webbasierte Lernumgebungen wie Bettermarks und mathe-online.at können gut als Ergänzung und zum individuellen und differenzierten Lernen genutzt werden.
Algodoo am Smartboard, Übung
Insgesamt war die Tagung inhaltlich nützlich, die Diskussionen leider eher technisch als didaktisch, da viele Lehrerinnen und Lehrer überhaupt erst erste Schritte mit verschiedener Software machten. Die Informatik war recht gut vertreten und auch einzelne bekannte Gesichter aus dem Umfeld der Educamps und Twitter-Community zu Bildung und Medien. Ich fand die einführende Präsentation der Tagung mit ein paar schicken 3D Bildern eher bunt aber nicht besonders zielführend und auch sonst zeigt sich mit überschaubaren Ausnahmen eine eher geringe Nähe von Lehrer/innen und Verantwortlichen im Schulkontext zu aktuellen Entwicklungen in der Informationstechnologie und den Möglichkeiten informatischer und medialer Werkzeuge. Hier laufen beispielsweise die Educamps erheblich anders mit der Session-Konzipierung und den direkten Vorstellungen der Workshops. Gut dagegen fand ich den Commsy-Raum, der vorbereitet war.
Auf der anderen Seite sind viele der interessanten Systeme auch nicht ohne weiteres kompatibel mit der Organisation Schule, wie sie derzeit stattfindet. Im Schulalltag sind die meisten mobilen Geräte, wie beispielsweise Handys, verboten oder werden zumindest weniger als Chance und eher als Bedrohung wahrgenommen. Ein „flipped classroom“ wäre in der Konsequenz auch flexibel genug, Schülerinnen und Schülern, die zuhause gut gearbeitet haben und keine weitere Fragen und Probleme mit dem Stoff haben, aus dem Unterricht zu entlassen, was gesetzlich derzeit nicht möglich ist. Außerdem gibt es viele organisatorisch unklare Rahmenbedingungen, was leider auch innovative Prozesse ausbremst. Aber insgesamt hat der Tag sich gelohnt, um über den Tellerrand zu schauen. Die Nutzung von i-Pads finde ich ziemlich spannend vom rein technisch-didaktischen Gesichtspunkt und ich konnte auch viele neue Erfahrungen mit den Geräten sammeln. Die Gegenargumente sind hinlänglich bekannt, Kosten und Apple…
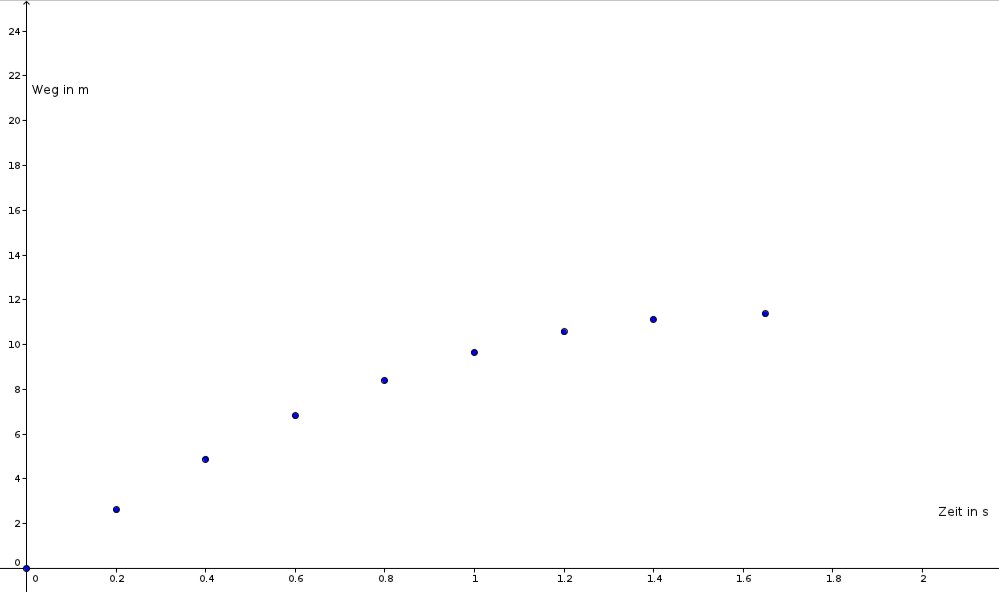
Am vergangenen Montag hatte ich eine Doppelstunde für eine problemorientierte Aufgabe in Mathematik in der Vorstufe mit Hospitation durch die Fachseminarleitung vorgesehen. Unter der Überschrift „Schafft ein Autofahrer es, bei 50 km/h Momentangeschwindigkeit rechtzeitig zu bremsen, wenn ein Reh 20 m vor dem Auto auf der Fahrbahn auftaucht?“ (mit einem vorgegebenen Richtwert für die Bremsverzögerung) sollte ein motivierender Anwendungsbezug für die Differentialrechnung über die Bestimmung eines Weges über die Momentangeschwindigkeit dargestellt werden.
Vorbereitet waren zusätzlich zur Überschrift mit einem plastischen Bild am Smartboard zwei Hilfekarten, die die beiden Grundformeln mit ihren Graphen enthielten. Nach einer längeren Gruppenphase sollten die Lösungswege und Lösungen auf Postern dargestellt und verglichen werden. Abschließend hatte ich zwei Grafiken vorgesehen, um den quadratischen Zusammenhang sowie die Abhängigkeit von der Oberflächenbeschaffenheit deutlich zu machen. Ein sehr physikalisches Thema also, anknüpfend an die vorangegangenen Stunden mit der Bestimmung der Momentangeschwindigkeit beim freien Fall.
Eine Grafik der ersten Hilfekarte
Die Motivation zum Thema war gelungen, es wurde über Faustformeln in der Fahrschule diskutiert und auch die Fragestellung an sich war deutlich. Allerdings zeigten sich in den meisten Gruppen sowohl Schwierigkeiten, sich der Problemstellung zu nähern, als auch die Gestaltung der Hilfekarten als zu abstrakt und zu wenig kleinschrittig. Die Darstellung auf Postern gelang nur zwei von vier Gruppen, allerdings konnten wir zum Ende der Stunde zumindest passable Ergebnisse diskutieren und günstiger Weise auch zwei Varianten erkennen. Eine Variante bezog die Reaktionszeit mit ein, die andere nicht. Dies führte zu verschiedenen Ergebnissen und ich griff die Situation auf, um zu verdeutlichen, dass es beim Problemlösen verschiedene Lösungen geben kann und nicht eine Musterlösung vorgesehen ist. Klar ist das eine Modell genauer als das andere, aber falsch ist keine von beiden.
In der Reflexion habe ich einerseits festgestellt, dass ich die Ergebnisse auf jeden Fall in den weiteren Stunden aufgreifen muß, um Klarheit zu schaffen. Als zweites habe ich mich gefragt, ob ich nicht eher Physik als Mathe im Vordergrund der Problemstellung hatte. Aber die beiden Bereiche sind auch sehr eng miteinander verwandt und ich werde im folgende Unterricht darauf achten, dass es nicht physikalisch bleibt. Hier bieten sich vor allem wirtschaftliche Zusammenhänge als Anwendungsgebiet an. Die Kommunikation lief meiner Ansicht nach gut und es gab jederzeit Klarheit, was zu tun ist und meine Hilfsbereitschaft. „Nachsteuerung ist Normalgeschäft“sowie „Problemlösen ist kein Selbstgänger sondern muß systematisch erlernt werden“ sind zwei der Konsequenzen aus diesem relativ offenen Unterrichtsexperiment für mich. Eine Frage für die weitere Arbeit als Lehrer sind meine Kommunikationsprinzipien in Gruppenarbeitsphasen sowie dem Einplanen von mehr Raum für Klärungsprozesse.
In der darauffolgende Stunde habe ich zum einen eine Kopie zum Thema „Problemlösen im Mathematikunterricht“ verteilt als auch das Thema Bremsweg mit Material von Fahrschulen und Beispieldaten sowie den erstellten Postern aufgegriffen. Hier wurde auch von einem Schüler problematisert, wie sehr die Faustformel von den berechneten Werten abwich, wobei ich herausstrich, dass Faustformeln immer „auf Nummer sicher“ erstellt werden, also lieber mehr Zeit und Strecke einplanen, als physikalisch bei optimalen Bedingungen angemessen. Die beiden Grafiken, die ich für den Vortag vorgesehen hatte, hatte ich leider nicht kopiert und konnte sie im Klassenraum auch nicht per Beamer zeigen. Allerdings konnten wir anhand der Berechnungen für 30 km/h und 70 km/h, die am Montag als Zusatz gedacht waren, den Rechenweg noch einmal systematisch festigen.
Material: UE-Bremsweg für den Blog