Am vergangenen Montag hatte ich eine Doppelstunde für eine problemorientierte Aufgabe in Mathematik in der Vorstufe mit Hospitation durch die Fachseminarleitung vorgesehen. Unter der Überschrift „Schafft ein Autofahrer es, bei 50 km/h Momentangeschwindigkeit rechtzeitig zu bremsen, wenn ein Reh 20 m vor dem Auto auf der Fahrbahn auftaucht?“ (mit einem vorgegebenen Richtwert für die Bremsverzögerung) sollte ein motivierender Anwendungsbezug für die Differentialrechnung über die Bestimmung eines Weges über die Momentangeschwindigkeit dargestellt werden.
Vorbereitet waren zusätzlich zur Überschrift mit einem plastischen Bild am Smartboard zwei Hilfekarten, die die beiden Grundformeln mit ihren Graphen enthielten. Nach einer längeren Gruppenphase sollten die Lösungswege und Lösungen auf Postern dargestellt und verglichen werden. Abschließend hatte ich zwei Grafiken vorgesehen, um den quadratischen Zusammenhang sowie die Abhängigkeit von der Oberflächenbeschaffenheit deutlich zu machen. Ein sehr physikalisches Thema also, anknüpfend an die vorangegangenen Stunden mit der Bestimmung der Momentangeschwindigkeit beim freien Fall.

- Das Tafelbild zum Einstieg
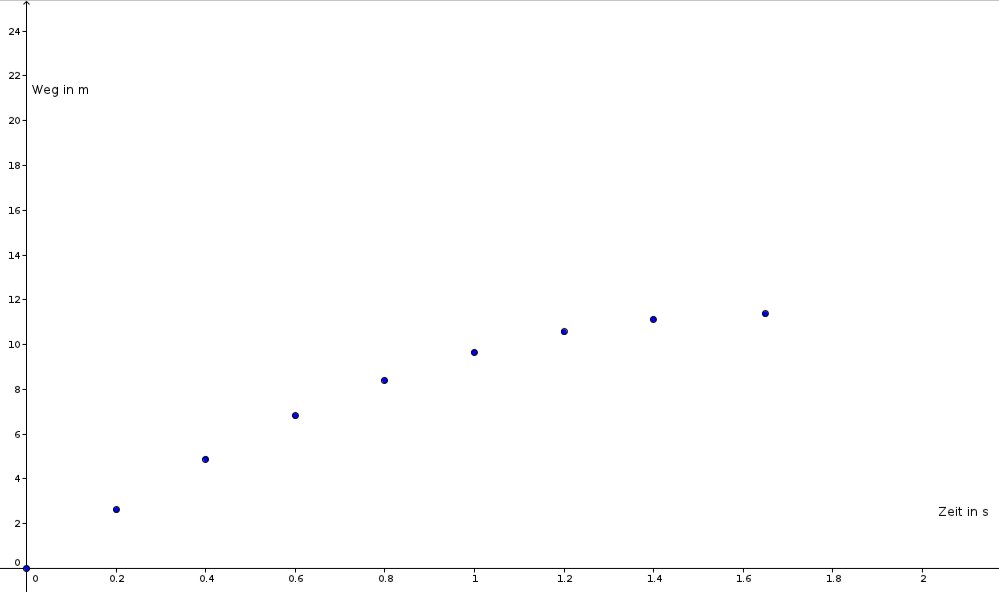
Eine Grafik der ersten Hilfekarte
Die Motivation zum Thema war gelungen, es wurde über Faustformeln in der Fahrschule diskutiert und auch die Fragestellung an sich war deutlich. Allerdings zeigten sich in den meisten Gruppen sowohl Schwierigkeiten, sich der Problemstellung zu nähern, als auch die Gestaltung der Hilfekarten als zu abstrakt und zu wenig kleinschrittig. Die Darstellung auf Postern gelang nur zwei von vier Gruppen, allerdings konnten wir zum Ende der Stunde zumindest passable Ergebnisse diskutieren und günstiger Weise auch zwei Varianten erkennen. Eine Variante bezog die Reaktionszeit mit ein, die andere nicht. Dies führte zu verschiedenen Ergebnissen und ich griff die Situation auf, um zu verdeutlichen, dass es beim Problemlösen verschiedene Lösungen geben kann und nicht eine Musterlösung vorgesehen ist. Klar ist das eine Modell genauer als das andere, aber falsch ist keine von beiden.
In der Reflexion habe ich einerseits festgestellt, dass ich die Ergebnisse auf jeden Fall in den weiteren Stunden aufgreifen muß, um Klarheit zu schaffen. Als zweites habe ich mich gefragt, ob ich nicht eher Physik als Mathe im Vordergrund der Problemstellung hatte. Aber die beiden Bereiche sind auch sehr eng miteinander verwandt und ich werde im folgende Unterricht darauf achten, dass es nicht physikalisch bleibt. Hier bieten sich vor allem wirtschaftliche Zusammenhänge als Anwendungsgebiet an. Die Kommunikation lief meiner Ansicht nach gut und es gab jederzeit Klarheit, was zu tun ist und meine Hilfsbereitschaft. „Nachsteuerung ist Normalgeschäft“sowie „Problemlösen ist kein Selbstgänger sondern muß systematisch erlernt werden“ sind zwei der Konsequenzen aus diesem relativ offenen Unterrichtsexperiment für mich. Eine Frage für die weitere Arbeit als Lehrer sind meine Kommunikationsprinzipien in Gruppenarbeitsphasen sowie dem Einplanen von mehr Raum für Klärungsprozesse.
In der darauffolgende Stunde habe ich zum einen eine Kopie zum Thema „Problemlösen im Mathematikunterricht“ verteilt als auch das Thema Bremsweg mit Material von Fahrschulen und Beispieldaten sowie den erstellten Postern aufgegriffen. Hier wurde auch von einem Schüler problematisert, wie sehr die Faustformel von den berechneten Werten abwich, wobei ich herausstrich, dass Faustformeln immer „auf Nummer sicher“ erstellt werden, also lieber mehr Zeit und Strecke einplanen, als physikalisch bei optimalen Bedingungen angemessen. Die beiden Grafiken, die ich für den Vortag vorgesehen hatte, hatte ich leider nicht kopiert und konnte sie im Klassenraum auch nicht per Beamer zeigen. Allerdings konnten wir anhand der Berechnungen für 30 km/h und 70 km/h, die am Montag als Zusatz gedacht waren, den Rechenweg noch einmal systematisch festigen.
Material: UE-Bremsweg für den Blog