Kleine Mathematik-Überlegungen auf Reisen

 Mathematik-Unterricht  No Responses »
Aug 252014
 

Während der letzten Monate und besonders nun, wenige Tage vor Schulbeginn habe ich mir immer mal wieder Gedanken zu kleinen Mathematik-Projekten oder -Aufgaben gemacht, die ich hier vorstellen möchte. Es geht gar nicht um besonders innovative Konzepte, sondern eher spontane Überlegungen, an denen ich getüftelt hatte. Dabei war mir weniger die konkrete Ausgestaltung wichtig, als Impulse festzuhalten.

  • Irgendwo unterwegs: Aus Temperaturtdiagrammen einer frei wählbaren Stadt der Welt (z.B. über Smartphones/Internetbrowser oder Lehrerrecherche) eine Tabelle erstellen und umgedreht, danach vergleichen und evt. über Wahl der Städte sprechen. Ziel dieser Aufgabe ist, Gesprächsanlässe und positive Bezugnahme auf Migrationshintergründe auch im Mathematikunterricht zu geben.
  • bei Mendoza, Argentinien im Weinanbau-Gebiet:
    1.) Weinreben werden etwa in einem Abstand von 1m voneinander gepflanzt. Wieviele Reben passen etwa auf 1 ha Land? (1ha = 100m x 100m)
    Am Rand des Grundstückes soll ein Abstand von jeweils etwa 1,50m für einen Weg gelassen werden.
    2.) Pro Weinrebe ergibt sich ein Ertrag von durchschnittlich 3 kg Trauben. (Erfahrungswert) Ein LKW kann maximal 5t transportieren. Wieviele ha Weinfelder lasse sich mit einem solchen LKW abtransportieren?
    3.) Angenommen, die gesamte Ernte des 1ha Weinreben-Feldes passt auf einen LKW. Wieviele kg Trauben ergaben sich für diese Ernte pro Weinrebe durchschnittlich?
    Lösungsideen: Zu 1.) Skizze machen, dann ergeben sich 98 x 98= 9604 Reben. Zu 2.) 9600 x 3kg = 28,8 t. Damit braucht es schon für 1 ha etwa 6 LKW-Fahrten. Zu 3.) 5000 kg: 9600 = ca. 0,5 kg
  • In der heissen Mittagspause bei Mendoza:
    1.) 6 Freunde wollen 2 Melonen teilen. In wieviele Teile schneiden sie die Melonen am einfachsten? Gibt es mehrere Möglichkeiten?
    2.) Emma backt Pfannkuchen. Für 10 Pfannkuchen braucht sie etwa 300 ml Milch. Die Packung hat 1,5l. Welcher Anteil ist nach dem Backen noch übrig, wenn sie vorher voll war? Wieviele Pfannkuchen könnte sie mit der ganzen Milch backen? (Wenn alle anderen Zutaten auch da sind!)
  • In Santiago im Park:
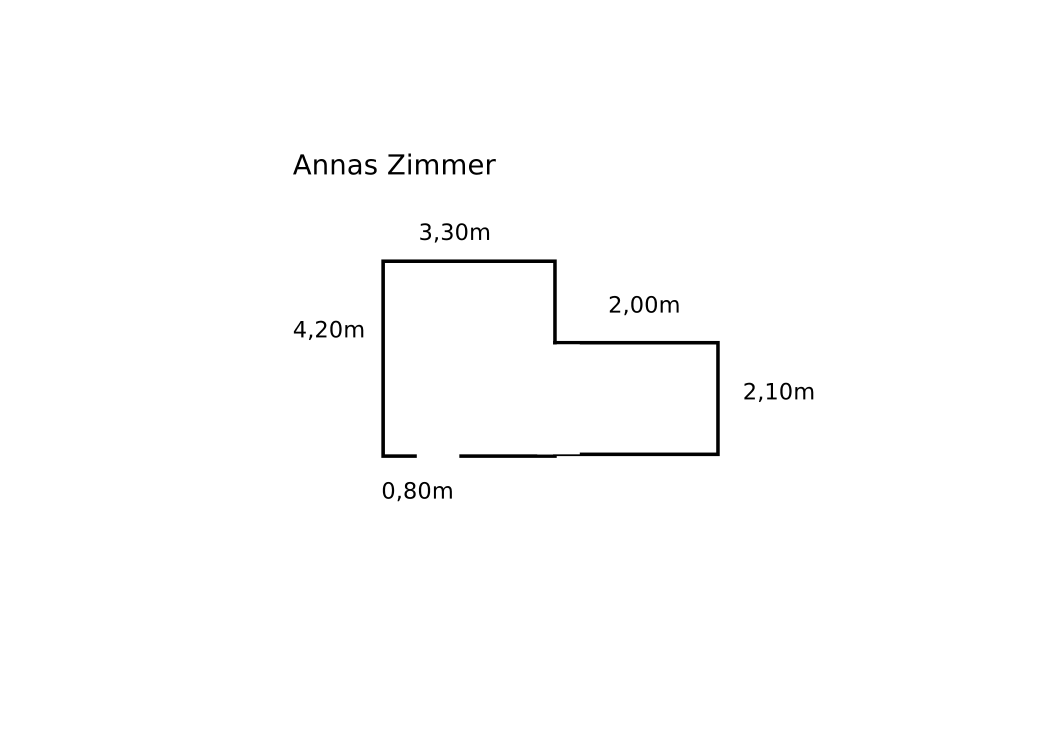
    Anna möchte ein Sofa kaufen. Welches Sofa passt am Besten ins Zimmer? Wo würdest Du es hinstellen? (Es gibt verschiedene Möglichkeiten)
    Sofa A : 0,7m x 2,2m        Sofa B: 0,8m x 1,9m     Sofa C: 0,7m x 2,0m

[Mathe Unterricht] „Passt der LKW durch den Tunnel?“ – quadratische Funktionen

 Allgemein, Mathematik-Unterricht, Referendariat  No Responses »
Sep 032012
 

Da ich mich gerade im Referendariat befinde, veröffentliche ich auch Teile meiner Auseinandersetzung mit der Ausbildung auf diesem Blog.

Vor einigen Tagen habe ich eine Hospitation in der Vorstufe (Klasse 11)  in Mathe durchgeführt und mich dabei unserem derzeitigen (Wiederholungs-)Unterrichtsgegenstand „quadratische Funktionen“ problemorientiert genähert. Gar nicht so einfach, wie ich finde, wo quadratische Funktionen im Alltag nicht so üblich zu finden sind wie geometrische oder stochastische Figuren und Konzepte.

Angelehnt an den schriftlichen Überprüfungen Mathematik (pdf) der Klasse 10 in Hamburg  habe ich mich dem Thema „Brückenbau“ genähert und eine gelungene Problemstellung gefunden, die sich in verschiedener Ausprägung häufiger auch im Netz findet (wenn bei google „brücke parabel lkw aufgabe“ eingegeben wird, erscheinen einige Treffer zu ähnlichen Aufgaben)

Die Problemstellung sollte allerdings durch einen stummen Impuls mit Bild von den Schüler/innen selbst gefunden werden, was auch relativ gut klappte, dann aber zu wenig im Unterrichtsgespräch fokussiert wurde.

„Wie hoch muss eine parabelförmige Brücke konstruiert werden, damit ein LKW gut hindurchpasst?“

Fachlich ist das Problem über die Auswahl einer günstig gestauchten Parabelform zu lösen, für die dann entsprechend ein Funktionswert zu gegebener Breite berechnet wird, der den Höhenabschnitt von LKW Oberseite zum Tunnel-Scheitelpunkt im Betrag ergibt. Eine hohe Hürde stellt die Modellierung dar, aber das mathematische Problem ist im Grunde genommen eine Wiederholung aus der Mittelstufe.

Ich veröffentliche hier auch meinen Unterrichtsentwurf in Teilen, personenbezogene Daten selbstverständlich nicht. Gerade in der Anzahl der Lernziele (viel zu Viele) und in der Genauigkeit der Verlaufsplanung könnte der Unterrichtsentwurf noch einmal kritisch überarbeitet werden. Bei einer offenen Problemstellung muss man auch immer damit rechnen, dass völlig andere als die intendierten Vorschläge zum Thema werden, beim hier eingesetzten Bild beispielsweise Geschwindigkeiten oder geometrische Aspekte. Dabei sollte das „Ostereierraten“ vermieden werden, indem auch nicht-intendierte Vorschläge entsprechend gewürdigt werden, aber das Thema der Unterrichtsstunde im Unterrichtsgespräch fokussiert werden. Ich habe mir auch vorgenommen, die Selbstreflexion anders aufzubauen, entweder mit abhak-Kästchen oder mit mehreren Abstufungen zum ankreuzen statt wie in diesem Material geplant mit offenen Feldern. Aber bei allen selbstkritischen Überlegungen, vielleicht hilft er ja der einen oder dem anderen beim Schreiben solcher Entwürfe oder beim Durchführen eines ähnlichen Unterrichtsbausteines.

Materialien:

UE-Morisse-28.08-fuer-blog.odt

Hilfekarten.pdf

zusätzliche-Problemstellungen.pdf

reflexion-mathe-vs.pdf

[Informatik-Unterricht] Reflexion Startmodul Informatik

 Allgemein, Informatik-Unterricht, Referendariat  No Responses »
Jan 122012
 

Am Donnerstag, den 15.12. habe ich unsere Unterrichtsplanung für die 9.Klasse im Themenbereich Robotik umgesetzt und wurde von meiner Fachseminarleitung und den Mitgliedern meiner Kleingruppe im Fachseminar Informatik hospitiert.
Ich habe die ersten drei Stunden unterrichtet, nachdem ich die Woche zuvor bereits 5 Stunden am Donnerstag im Kurs unterrichtet hatte. In den ersten beiden Stunden ging es um die Leitfrage „Wie orientiert sich eine Roboter?“, im zweiten Teil in der dritten und vierten Stunde um das Problem „Orientierung eines Roboters im Labyrinth„. Continue reading »