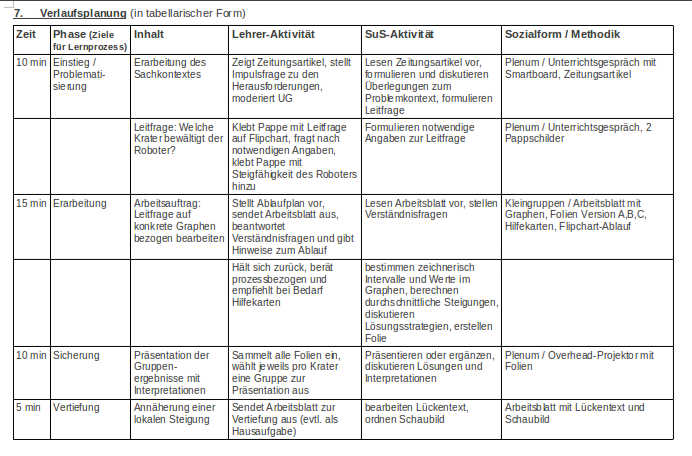
Als Gegenstand zur Vorbereitung der lokalen Änderungsrate habe ich gestern eine Stunde in der Vorstufe durchgeführt, die problemorientiert die Ermittlung von Steigungen auf verschieden großen Intervallen eines Graphen motivierte. Anhand eines aktuellen Zeitungsartikels zu geplanten Roboter-Einsätzen auf dem Mond, um in tiefen Kratern nach Wasser zu suchen wurde die Leitfrage aufgeworfen, welche Krater ein solcher Roboter mit einer gewissen Steigfähigkeit wieder verlassen kann. Anhand gegebener Graphen ermittelten die Schüler/innen zeichnerisch mehrere durchschnittliche Steigungen und präsentierten diese per Overhead-Folie. Trotz moderner Medien habe ich mich für die Arbeit mit solchen Folien entschieden, da sie während der Erarbeitung in Gruppen problemlos nebenbei gestaltet werden können. In der anschließenden Diskussion wurde thematisiert, wie eine maximale Steigung angenähert werden kann, um damit die lokale Änderungsrate als Ergebnis einer Grenzwert-Betrachtung immer kleinerer Intervalle zum Differenzenquotienten vorzubereiten. Abschließend wurde das Erlernte mit einem einfachen Lückentext und einer Hausaufgabe gesichert.
Als Aufhänger verwendete ich einen Zeitungsartikel zum Roboter-Einsatz auf dem Mond vom Handelsblatt. Das Deutsche Forschungszentrum für Künstliche Intelligenz (DFKI) forscht in Bremen seit Jahren an Robotern, die möglichst energiesparend und beweglich für Forschungen auf dem Mond eingesetzt werden sollen. Durch eine Impulsfrage von mir als Lehrer zu den Herausforderungen eines solchen Robotereinsatzes auf dem Mond sollten die Schüler/innen sich eigenständig der Leitfrage nähern, aber auch weitere wichtige Fragen im Kontext darstellen können.
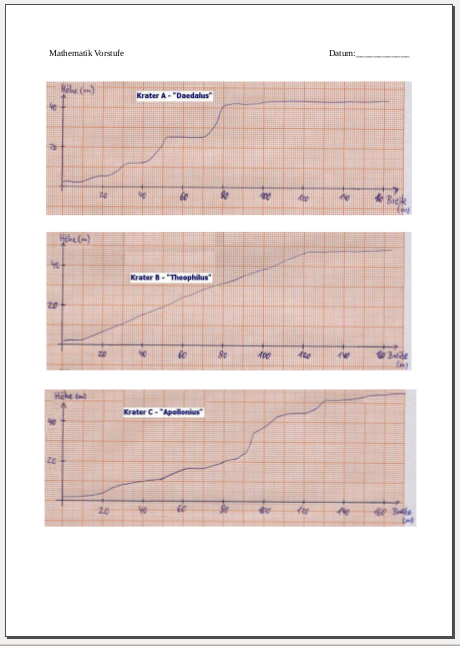
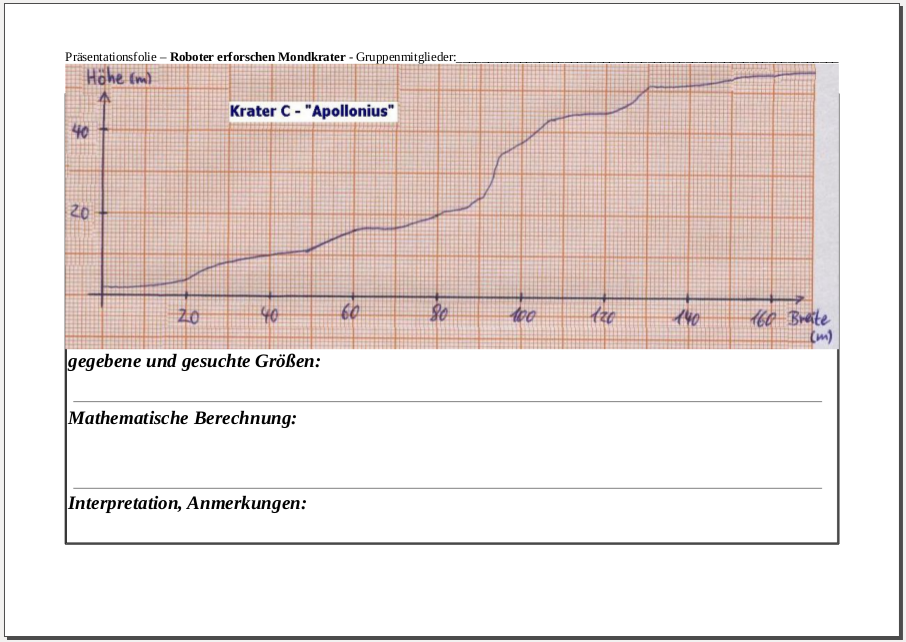
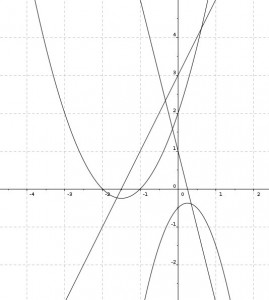
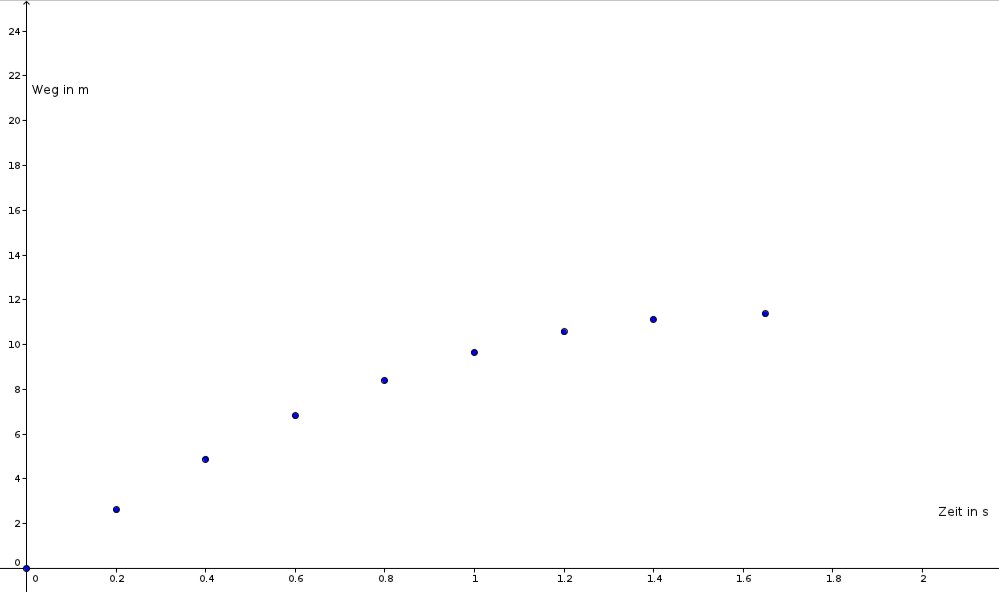
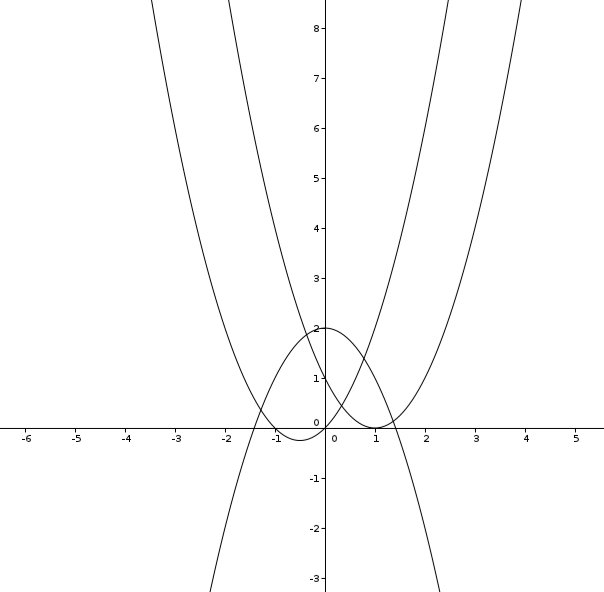
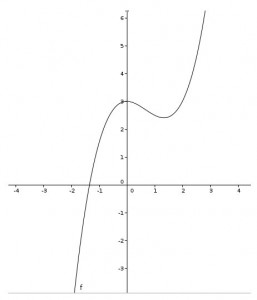
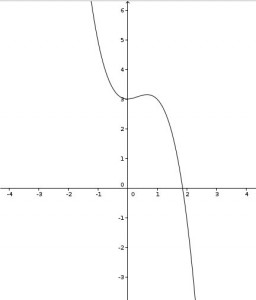
Ich habe mich entschieden, den Schüler/innen drei Graphen zur Betrachtung zu geben, um einerseits motivierende Teilergebnisse zu sichern, da zwei der drei Graphen bereits sehr schnell eindeutige Aussagen zulassen. Der dritte Graph sollte dann analog zu den einfacheren ersten beiden bearbeitet werden und ist so konzipiert, dass er höhere Anforderungen mit sich brachte. In erster grober Näherung liegt die Steigung des dritten Kraters unter der Steigfähigkeit des Roboters, auf einigen kleinen Intervallen ist die Steigung dann aber über dieser, so dass er diesen Krater nicht verlassen kann. Somit wurde den Schüler/innen durch die Aufgabenstellung nahegelegt, kleinere Intervalle zu betrachten.
(Bildnachweise für das Arbeitsblatt: Roboter-Screenshot vom DFKI, Mondkrater unter public domain von der NASA)
(Bildnachweise: Eigene Produktion)
In der Nachbetrachtung hat sich das Problem des Roboter-Einsatzes als Unterrichtsgegenstand gelohnt, die Schüler/innen waren interessiert bei der Sache und die Leitfrage war einfach verständlich und damit der Arbeitsauftrag klar. Nach der Präsentation zielte ich mit einer Frage zur notwendigen, hypothetischen Steigfähigkeit eines Roboters zur Bewältigung eines gegebenen Kraters auf die Ermittlung der maximalen Steigung des Graphen. Diese kann nur als punktuelle Steigung sicher berechnet werden und somit wurde die Betrachtung lokaler Steigungen in den folgenden Stunden vorbereitend motiviert.
Materialien:
Arbeitsblatt-Gruppenarbeit (pdf)
Folie-A (pdf)
Folie-B (pdf)
Folie-C (pdf)
Arbeitsblatt-Lueckentext (pdf)
Arbeitsblatt-Hausaufgabe (pdf)