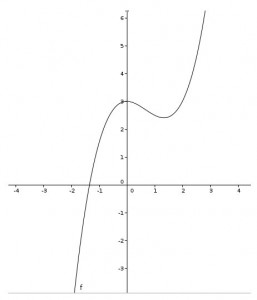
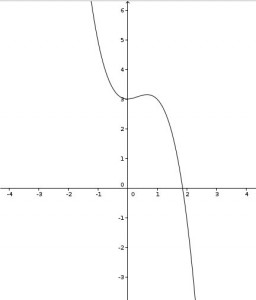
Als Vorbereitung auf den zentralen Begriff der Differentialrechnung, die Ableitung, habe ich die letzten Wochen im Mathematik-Unterricht der Vorstufe die Interpretation von Wertetabellen und Graphen geübt. Mit einer Aufgabe, die als Extremwertaufgabe mit der Ableitung direkt lösbar wäre, habe ich den Tiefpunkt per Wertetabelle und per grafischer Abschätzung bestimmen lassen. Die Aufgabe hierzu (Horizontalflug) habe ich von einem Kollegen empfohlen bekommen. Sie sind auch online erhältlich bei Frank Nordheim, der (seinen Schüler/innen) auch weitere Materialien zur Verfügung stellt.
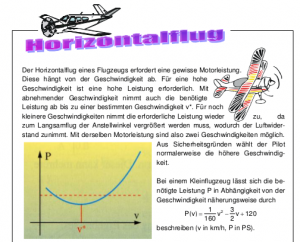
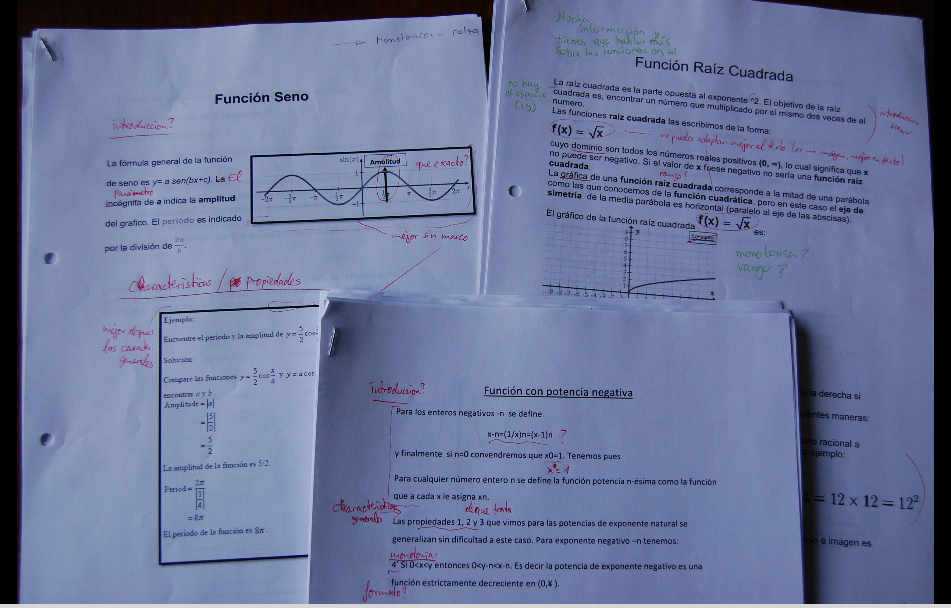
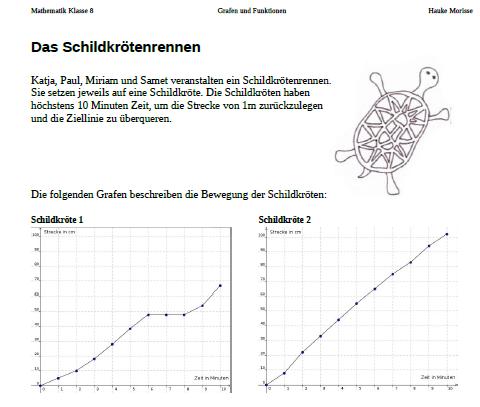
ein Ausschnitt aus dem Material von Frank Nordheim
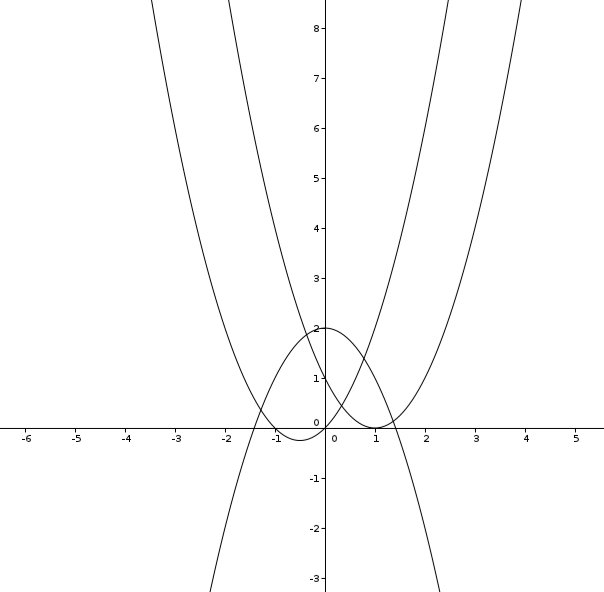
Die Aufgabe hierzu war, den Graphen zur Funktionsgleichung zu zeichnen, die Geschwindigkeiten zu einer gegebenen Leistung zu bestimmen sowie die Geschwindigkeit zur minimalen Leistung. Es gab Schwierigkeiten der Schüler/innen, zu erkennen, dass mit einer Ausnahme immer zwei Geschwindigkeiten zu einer Leistung gehören, da „wenn ich in die Formel nur eine Leistung einsetze ja auch nur eine Geschwindigkeit da steht“ Rechnerisch gehören bei einer quadratischen Funktion überwiegend zwei Lösungen zu einem Funktionswert, wobei scheinbar auch der Sachkontext verwirrte, in dem festgelegt war, dass für einen Flug mit sehr langsamer Geschwindigkeit ebenfalls höhere Leistung benötigt wird. Auch der Wechsel von einer „klassischen“ quadratischen Gleichung mit x und y als Variablen zu v und P(v) gestaltete sich als Hürde. Allerdings wurde in der Diskussion dann auch mit Hilfe einer geogebra-Visualisierung Klarheit geschaffen.
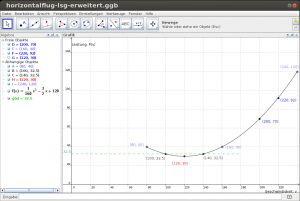
Eine Lösungsvariante zur Aufgabe
Im gleichen Kontext hatte ich vor, die Nützlichkeit von Tabellenkalkulations-Programmen zu zeigen, indem ich über eine Funktion, beispielsweise in Libre Office Calc Werte in immer kleineren Intervallen schachteln lasse. Hierzu bin ich zeitlich leider nicht mehr gekommen.
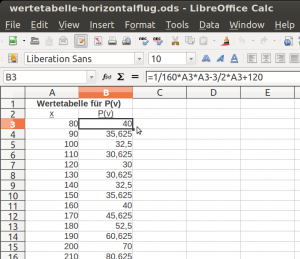
In einer Tabellenkalkulation lässt sich ein Extremwert durch Intervallschachtelung annähern, ohne eine Grafik erstellen zu müssen.
Zusätzlich habe ich als Wiederholung die beiden Punkte zur gegebenen Leistung von 32,5 Ps mit Hilfe der Funktionsgleichung und der quadratischen Ergänzung lösen lassen:
P(v) = 32,5 Ps = 1/160 v^2 – 3/2 v + 120
v^2 – 240 v + 14000 = 0
usw.
Als Sicherung habe ich zwei Versionen eines Arbeitsblattes ausgegeben, das jeweils die Lösung auf der anderen Version vorgegeben hat, um die Vernetzung der Darstellungsformen Wertetabelle und Graph zu stärken.
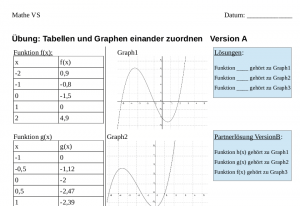
Ausschnitt des Arbeitsblattes Version A
Hier sind die Materialien zum weiterverwenden: Material-Darstellung-Tabelle-Graph.zip