[Mathe Unterricht] Differentialrechnung und Geogebra

 Allgemein, Lernwerkzeuge, Mathematik-Unterricht, Referendariat  No Responses »
Apr 222012
 

In den letzten Wochen habe ich in meinem Vorstufen-Kurs mehrmals die dynamische Geometriesoftware Geogebra eingesetzt.

Zum einen für Demonstrationen vorne am Smartboard, zum anderen zur eigenständigen Bearbeitung von dynamischen Arbeitsblättern und schlussendlich auch zur Erzeugung von Grafiken per Screenshot für Papierarbeitsblätter und eine Klassenarbeit.

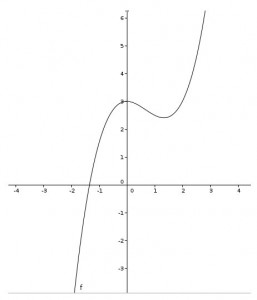
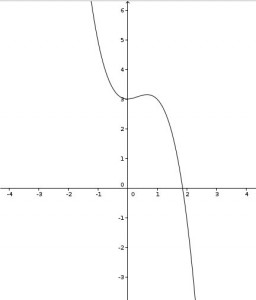
Zur Demonstration des grafischen Ableitens habe ich ein bereits verfügbares dynamisches Material verwendet, das die Tangentensteigung als Spur markiert:

http://www.geogebratube.org/material/show/id/1291

Hier habe ich ein eigenes Arbeitsblatt entwickelt, dass die Möglichkeiten von Geogebra allerdings bei weitem nicht ausschöpft:
http://www.geogebratube.org/material/show/id/6972

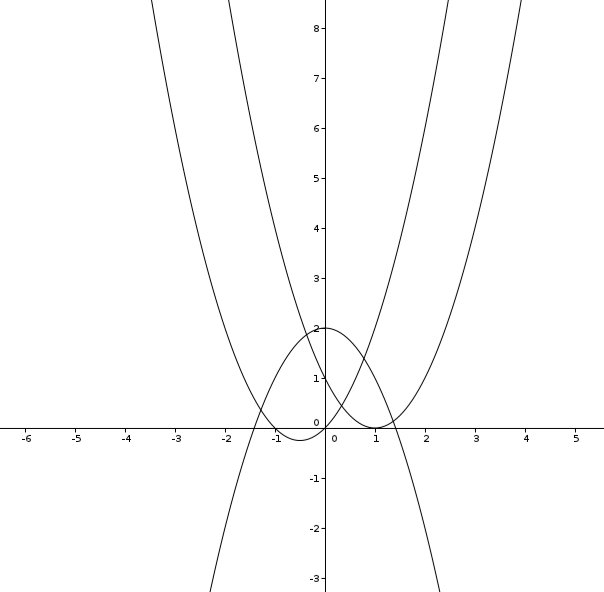
Und hier ist einer der Screenshots mit dazugehörigem Arbeitsblatt:

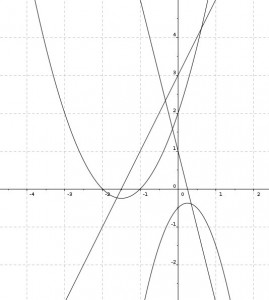Arbeitsblatt (OpenOffice Datei)

Arbeitsblatt (pdf Datei)

Und die Aufgabe aus der Klausur (wobei ich die Skalierung ungeschickt gewählt hatte, da hätte ich besser von -7 bis +7 als y Bereich wählen sollen:

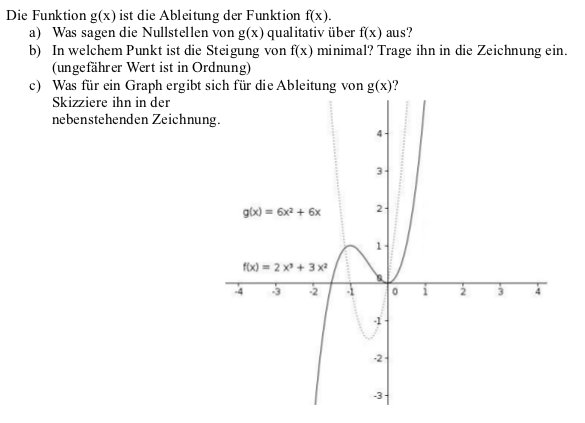Insgesamt ist das Arbeiten mit Geogebra vor allem für dynamische Zusammenhänge sehr nützlich und sowohl für Präsentationen von Konzepten als auch zur selbstständigen Bearbeitung sehr hilfreich. Zur Erarbeitung didaktisch passender dynamischer Materialien braucht es etwas Zeit, aber es gibt auch schon eine ganze Reihe frei verfügbarer Materialien, die in ein Unterrichtsvorhaben eingebettet werden können.

Zum anstehenden Thema Kurvendiskussion in meinem Kurs werde ich beispielsweise sicher auf das Material Differentialrechnung – Wendepunkte – Sachsenringkurve verwenden. 

[Mathe Unterricht] Einstieg in die Differentialrechnung

 Allgemein, Mathematik-Unterricht, Referendariat  No Responses »
Feb 092012
 

Ich habe seit dem 1.Februar nun bedarfsdeckenden Unterricht und daher nicht ganz so viel Zeit, viel zu schreiben. Für den Mathematik Unterricht in der Vorstufe habe ich ein paar Grafiken mit Geogebra vorbereitet und auch den Zusammenhang zwischen den Tangentensteigungen an einer Parabel und der ersten Ableitung mit Hilfe eines netten dynamischen Arbeitsblattes visualisieren können. Als „Aufwärmübung“ habe ich Graphen und Funktionsgleichungen vorgegeben, die zugeordnet werden sollten (siehe Screenshots unten)

Ordne die Funktionen den Graphen zu
f ( x)=x^2+x
g(x)=(x−1)2
h(x )=−x^2+2

Ordne die Funktionen den Graphen zu

f (x)=0,5 x^3−x^2+3
g( x)=−x^3+x^2+3