Nach einem ersten Anlauf, der leider etwas ungenau geplant war, hatte ich heute die Möglichkeit, eine Doppelstunde zur Einführung in das Konzept der Vererbung in der objektorientierten Programmierung ein zweites mal besser vorstrukturiert durchzuführen.
Das Möbelplaner-Projekt wurde die letzten Jahre von Hamburger Informatik-Lehrer/innen und Didaktiker/innen, unter anderem von meinem Kollegen Uwe Debacher als möglicher Anwendungskontext für den Themenbereich „Objektorientierte Programmierung“ im Rahmenplan der Studienstufe in Hamburg in Java entwickelt.
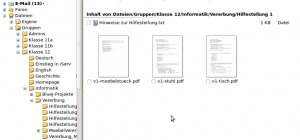
Das Projekt ist für die IDE (integrierte Entwicklungsumgebung) BlueJ konzipiert und besteht aus einer Klasse „Leinwand“, die die anspruchsvolleren Aufgaben der grafischen Darstellung im Hintergrund übernimmt, und aus den Klassen „Stuhl“ und „Tisch“, die sich auf die Leinwand zeichnen lassen. Mit diesem Projekt arbeiten wir den Großteil des Semesters und bauen die Funktionalitäten Schritt für Schritt aus.
Grafik übernommen von http://www.debacher.de/wiki/BlueJ
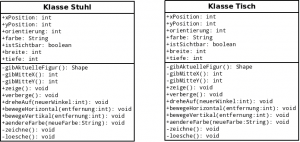
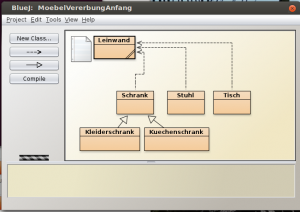
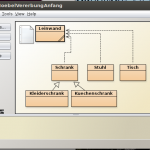
Als Einstieg in das Thema „Vererbung“ wählte ich ein UML-Diagramm (eine standardisierte Beschreibungssprache) der beiden Klassen „Stuhl“ und „Tisch“, um die Attribute und Methoden wirkungsvoll im Vergleich gegenüberzustellen. Genauer wurde UML an dieser Stelle nicht thematisiert, dies werde ich im laufe der nächsten Wochen genauer tun.
eigene Grafik
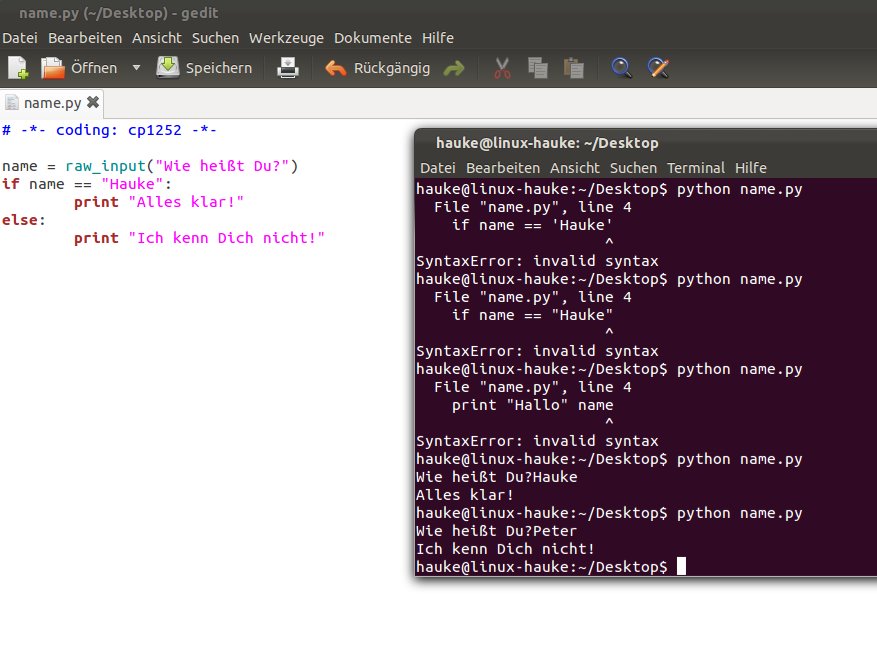
In Hinblick auf Wartbarkeit und Übersichtlichkeit von Software diskutierten wir die Nachteile von Code-Dopplungen. An einem vorbereiteten Beispiel „Schrank“ mit erbenden Klassen „Kleiderschrank“ und „Küchenschrank“ habe ich daraufhin das Konzept in Java gezeigt, wie sich Objekte erzeugen lassen und Attribute wie Methoden von „Schrank“ auf die beiden Spezialfälle übertragen lassen, indem diese mit dem Schlüsselwort „extends“ als Unterklassen von Schrank definiert werden. (siehe weiter unten „Schrank.zip“ für das vollständige Java-Projekt) Hierbei habe ich extra-Zeit verwendet auf die Klassifizierung von Compiler-Fehlern und dabei auch das Thema Sichtbarkeit von Attributen und Methoden im Kurs diskutiert: Die zu vererbenden Elemente müssen als „public“ oder besser als „protected“ umgeschrieben werden, damit die erbenden Klassen auf diese zugreifen können.
Die Klasse Schrank mit den erbenden Unterklassen Kleiderschrank und Kuechenschrank, eigene Grafik
„Schrank“ und „Kleiderschrank“ sowie „Kuechenschrank“ als UML-Diagramm, eigene Grafik
Die Aufgabenstellung war nun, für das eigene Möbelplaner-Projekt die Klassen Stuhl und Tisch (und möglicherweise weitere Klassen) von einer generalisierenden Oberklasse „Moebelstueck“ erben zu lassen, um den Quellcode zu reduzieren und das Erzeugen neuer Möbel-Klassen zu erleichtern.
Hierzu hatte ich in unserem schulinternen Server-System mit iServ mehrere Hilfestellungen in Form von Quellcode als pdf je Klasse in verschiedenen Entwicklungsstufen mit einer Beschreibung des aktuellen Schrittes zur Verfügung gestellt, aber erst, nachdem alle etwa 20 Minuten eigenständig am arbeiten waren, um diejenigen zu unterstützen, die große Schwierigkeiten mit der Aufgabe hatten.
Das Hilfesystem mit schrittweisen Versionen der erbenden und vererbenden Klassen.
Etwa 20 Minuten vor Schluss habe ich einen Schüler, der gut in der Zeit lag sein Zwischenergebnis präsentieren lassen, um an diesem die Konfliktstelle zu diskutieren, die mir beim ersten Versuch im Parallelkurs den Rahmen gesprengt hatte. Die Methode „gibAktuelleFigur()“ erzeugt über einen GeneralPath eine zweidimensionale grafische Darstellung der betreffenden Klasse. Wenn nun sämtliche Methoden aus „Stuhl“ und „Tisch“ generalisiert werden, so muss auch die Methode „gibAktuelleFigur()“ in Moebelstueck enthalten sein, da sie von anderen Methoden benötigt wird, die exakt gleich sind in „Stuhl“ und „Tisch“. Dies hatte der Schüler selbst als „unschön“ gelöst erkannt, dass er einfach wie beim Stuhl einen Shape erzeugen ließ, obwohl ein Möbelstück gar keine direkte Form haben kann. Daran anknüpfend zeigte ich den Schüler/innen an der Schülerlösung, wie eine abstrakte Methode in einer dann abstrakt deklarierten Klasse eingefügt wird, die die Implementierung der Methode dann den Unterklassen überlässt. Dies rundete das heutige Thema ab und wurde gegen Ende der Stunde noch von einer Sicherungsphase mit individuellem Forumsbeitrag abgeschlossen.
Einige der Antworten auf die erste Fragestellung:
„Die Vererbung ist nützlich für das Software Projekt, weil es übersichtlicher gestaltet ist. Zwar braucht man Zeit um alles zu verstehen, doch nach und nach merkt man, dass es besser und schneller geht, wenn man die Sachen einmal definiert.“
„Es verkürzt das Schreiben um einiges und vereinfacht das Erstellen von Möbelstücken.“
„Die Vererbung ist sehr nützlich,weil man sich so eine Menge Arbeit sparen kann. Man definiert die Sachen die immer gleich sind nur ein einziges Mal. Außerdem wird es auch für den Aussenstehenden viel einfacher verständlich, weil das Skript nicht mehr so lang und kompliziert wirkt.Auch neue Klassen sind dank der Vererbung leichter zu erstellen.“
Die vollständigen Unterlagen zum weiterverwenden gibt es bei Uwe Debacher und soweit hier verwendet auch ausschnittsweise hier:
