[Mathe-Unterricht] Mathematische Modellierung in Mittel- und Oberstufe

Die Zeit vergeht, gut gefüllt und ohne neue Blogbeiträge. Unterricht, Klassenlehrer-Belange und Vater sein – dazu einige neue Herausforderungen wie wissenschaftliches Schreiben, Mitarbeiten an anderen Webplattformen wie Klexikon oder Serlo und die Content-Entwicklung im schuleigenen moodle, alles Tätigkeiten, die nicht direkt mit Veröffentlichungen und webbasiertem Arbeiten zu tun haben. Aber nun habe ich einen aktuellen Anlass, einmal zu schreiben.

Im Rahmen der in Hamburg vorgesehenen Präsentationsprüfungen im Abitur als Alternative zur mündlichen Prüfung habe ich in meinem S4 Kurs grundlegendes Niveau das Thema Modellierung ins Zentrum der letzten Stunden gerückt, da Realitätsbezüge mir auch besonders wichtig über das Abitur hinaus erscheinen und zur Unterstützung der zahlreichen Prüflinge, die sich nun kreativ anwendungsorientiert ein Thema der Mathematik für ihre Prüfung suchen.

Anregungen gibt es unter anderem in einer Handreichung des LI mit Beispielaufgaben, aber besonders die wesentlichen Prozesskompetenzen „argumentieren“ und „modellieren“ brauchen viel Übung, so dass ich verschiedene „Klassiker“ der mathematischen Modellierung aufgegriffen habe. Einer dieser Klassiker ist die Modellierung einer Wasserversorgung im Stau, mathematisch auf Mittelstufen-Niveau, aber dadurch mit Blick auf die prozessbezogenen Kompetenzen ein guter Einstieg / Wiederholung. Die Fragestellung lautet so oder ähnlich „Im Radio wird durchgesagt, dass sich vor Hamburg Richtung Norden ein Stau von 20 km Länge befindet. Wieviele Flaschen Wassen müssten zur Versorgung verteilt werden, wenn jede Person im Stau eine erhalten soll?“ Hier ist die mathematische Problemlösung auf einfache Grundrechenarten beschränkt, aber es müssen zahlreiche begründete Abschätzungen vorgenommen werden. Als weiteres Modellierungsproblem habe ich die „Stationierung von Rettungshubschraubern in Südtirol“ von Ortlieb und Kaiser übernommen und angewandt (siehe http://www.dr-gabriele-kaiser.de/media/files/Modellierung_final.pdf ab S.51), aber nur ansatzweise geometrisch in einer Doppelstude diskutiert. Die Problemzerlegung führte auf eine Minimierung von Abständen in Dreiecken und Fragen wie „Welcher Punkt hat in der Summe den kleinsten Gesamtabstand von allen Eckpunkten eines Dreiecks?“ und Diskussionen über Winkelhalbierende, Mittelsenkrechte und Schwerpunkt. Mithilfe von Geogebra wurden Extremsituationen von markanten Dreieckspunkten dargestellt, um sich den Fragestellungen zu nähern. Echtes kreatives mathematisches Denken statt einfacher Lösungsweg-Anwendung.

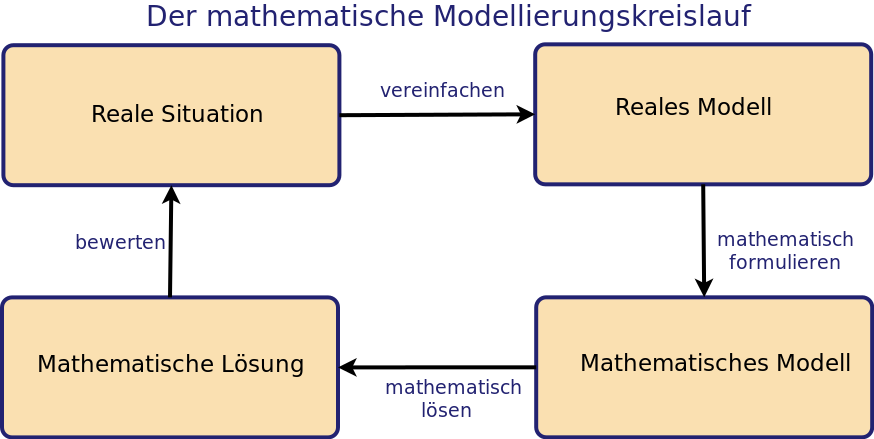
Nun ist ein banaler Grund, hier über Modellierung zu schreiben auch der, dass ich keine creative commons Grafik zum Modellierungskreislauf gefunden habe – daher habe ich diese schnell selbst erstellt und stelle sie hiermit (auch für andere Veröffentlichungen) zur Verfügung. Den Modellierungskreislauf habe ich in der Oberstufe verwendet, aber auch in der Mittelstufe, wo ich heute in Klasse 9 zum Thema Kreis Kabellängen abschätzen ließ, angelehnt an Greefrath (https://www.friedrich-verlag.de/shop/modellieren-lernen-mit-offenen-realitatsnahen-aufgaben) und Fotos von Kabelrollen (ähnlich dem dargestellten Foto)

(CC-BY-SA)

Hier noch einmal die Dateien zum Modellierungskreislauf (mit DIA erstellt)

Modellierungskreis-Grafik

Und Literatur / Links zum Thema Modellierung:

„Das Projekt: Modellierung in der Schule“ von u.a. Gabriele Kaiser: http://www.dr-gabriele-kaiser.de/media/files/Modellierung_final.pdf

Buch: „Modelllierung im Mathematikunterricht“ von Gerd Hinrichs: https://www.hugendubel.de/de/buch/gerd_hinrichs-modellierung_im_mathematikunterricht-7053090-produkt-details.html

Buch: „Mathematische Modellierung – eine Einführung in zwölf Fallstudien“ von u.a. Peter Ortlieb: http://www.springer.com/de/book/9783658005344

Buch: „Modellieren lernen – mit offenen realitätsnahen Aufgaben“ von Gilbert Greefrath: https://www.friedrich-verlag.de/shop/modellieren-lernen-mit-offenen-realitatsnahen-aufgaben