Nach zeitaufwändiger Organisation und Überprüfung, ob es möglich und sinnvoll sei, habe ich nun in meinen drei Physik-Kursen der 9.Klassen jeweils eine tagsfüllende Exkursion von Cuenca zu den beiden Wasserkraftwerken Mazar und Molino unternommen. Betrieben werden die beiden Kraftwerke sowie die gesamte Energieversorgung des Landes von der staatlichen Firma CELEC, die uns über einen Kontakt an der Schule eine formale Erlaubnis für die Besuche ausstellte. Mit 120 Hm3 Stausee-Volumen und einer Leistung von 1075 MW ist das zwischen 1976 bis 1991 erbaute Kraftwerk Molino das größte Kraftwerk des Landes Ecuador.
Diese Woche haben wir uns auf den kommenden Schulstart nächste Woche in Form von Konferenzen, Treffen und vielem mehr vorbereitet. Klar, das Vieles auf einem öffentlichen Blog keinen Platz hat und auch vertraulich ist, aber ein paar Eindrücke möchte ich hier festhalten.
Zunächst habe ich nun meine Unterrichtsverteilung fest, ich werde in der 10. und 11. Klasse Mathematik auf Spanisch unterrichten und Physik in der 9. auf Deutsch. Leider muss ich dieses Schuljahr darauf verzichten, Informatik zu unterrichten. Entgegen der Einschätzung vieler meiner Kolleg/innen in Deutschland (und meiner eigenen noch vor einigen Monaten) heißt Deutsche Auslandsschule nicht, dass alle Fächer auf Deutsch unterrichtet werden. Dies ist nur für das deutsche Abitur notwendig, das nicht von allen Deutschen Auslandsschulen vergeben wird.
In Cuenca kann neben dem ecuadorianischen „Baccilerato nacional“ das „Bachillerato Internacional Multilingüe (GIB) /International Baccalaureate“(IB) abgelegt werden, wie es an den Deutschen Auslandsschulen üblich ist, die kein deutsches Abitur anbieten. Für das IB gibt es Prüfungsfächer, die teilweise auf Deutsch, teilweise auf Spanisch sind sowie zusätzliche Vorgaben und Anforderungen. An unserer Schule ist Englisch und Deutsch Prüfungsfach, Mathematik auf Spanisch und Geschichte und Biologie auf Deutsch. In Mathematik wird eine Art Facharbeit / schriftliche Ausarbeitung zu einem selbstgewählten Thema verlangt. Es gibt auch eine ganze Menge Materialen zur Prüfungsvorbereitung, die weltweit zentral abgelegt wird, z.B. im online curriculum center der IB-Organisation. Hier wird einer meiner Schwerpunkte für das Schuljahr liegen, da ich in Mathematik der Klasse 11 viel mit der IB-Struktur zu tun haben werde.

Diploma Programme curriculum framework
Der deutschsprachige Fachunterricht (DFU) findet in der Secundaria (Mittelstufe) in Biologie, Geschichte und teilweise auch in anderen Fächern wie dieses Jahr bei mir in Physik 9.Klasse statt. Interessant ist hierbei, dass der Großteil der Kinder und Jugendlichen an unserer Schule Deutsch als Fremdsprache haben, so dass der Fachunterricht sehr sprachsensibel stattfindet. Gut ist, dass wir als Fachlehrer/innen im Austausch über Synergieeffekte in den Jahrgangsstufen sind und beispielsweise gezielt neue Begriffe aus anderen Fächern mit aufgreifen wollen. Besonders die Biologie bietet Überschneidungen mit meinem Unterricht. Eine umfangreiche Materialsammlung zum DFU gibt es im DFU-.Cockpit. Ich werde in meinem Physikunterricht am zentralen Begriff der Energie möglichst projektorientiert Grundlagen der Elektrotechnik, Maschinen und Energieumwandlung lehren und dabei auch Vokabellisten/Wortlisten nutzen.
Auzug einer Infografik von: http://www.socialphy.com/posts/off-topic/22032/Wonderful-World-Of-Energy-Infographic-Design.html
Die Mathematik in der 10.Klasse orientiert sich an einem Lehrwerk, zu dem es auch eine online-Plattform gibt: http://www.20enmate.com/ Hier werde ich zunächst diagnostizieren, wie weit die fachlichen Kompetenzen reichen, um dann darauf aufbauend auf die Oberstufen vorzubereiten. Zusatzangebote zu den Unterrichtsstunden stelle ich von Anfang an auf einem Blog bereit: http://mate10cuenca.wordpress.com/
Allgemein war die erste Woche sehr informativ und hat auch schon deutlich gemacht, welchen Herausforderungen wir gegenüberstehen. So müssen Deutsche Auslandsschulen nicht nur den Vorgaben deutscher Institutionen und Behörden genügen, wie der Bund- Länder- Inspektion (BLI) sondern auch den nationalen Vorgaben des ecuadorianischen Staates, beispielsweise bei der Anfertigung von Protokollen, Planungsunterlagen und der Einhaltung von Fristen zur regelmäßigen Notenvergabe in vorgegebenen Rastern. Als Privatschule spielen die Eltern eine andere Rolle als in einer staatlichen Schule. Zudem besteht das Kollegium aus Lehrer/innen, die im ecuadorianischen Bildungssystem groß geworden sind und anderen so wie ich, die bisher nur das deutsche Bildungssystem kennen, so dass auch kommunikativ, strukturell und interkulturell vieles anders läuft als an einer Schule in Deutschland. Die Konferenzen verlaufen beispielsweise immer zweisprachig und meine Fachschaftssitzungen nur auf Spanisch. Jedenfalls bin ich mir schon sicher, dass ich hier meine Spanischkenntnisse intensiv ausbauen werde und einiges über Fremd- und Eigenwahrnehmung lernen kann. Im Laufe der nächsten Woche werde ich nun auch meine Schüler/innen kennenlernen und meine ersten spanischsprachigen Unterrichtsstunden gestalten. Und es bleibt auch Zeit, die Gegend zu erkunden, beispielsweise den Cajas Nationalpark.
Während der letzten Monate und besonders nun, wenige Tage vor Schulbeginn habe ich mir immer mal wieder Gedanken zu kleinen Mathematik-Projekten oder -Aufgaben gemacht, die ich hier vorstellen möchte. Es geht gar nicht um besonders innovative Konzepte, sondern eher spontane Überlegungen, an denen ich getüftelt hatte. Dabei war mir weniger die konkrete Ausgestaltung wichtig, als Impulse festzuhalten.
- Irgendwo unterwegs: Aus Temperaturtdiagrammen einer frei wählbaren Stadt der Welt (z.B. über Smartphones/Internetbrowser oder Lehrerrecherche) eine Tabelle erstellen und umgedreht, danach vergleichen und evt. über Wahl der Städte sprechen. Ziel dieser Aufgabe ist, Gesprächsanlässe und positive Bezugnahme auf Migrationshintergründe auch im Mathematikunterricht zu geben.
- bei Mendoza, Argentinien im Weinanbau-Gebiet:
1.) Weinreben werden etwa in einem Abstand von 1m voneinander gepflanzt. Wieviele Reben passen etwa auf 1 ha Land? (1ha = 100m x 100m)
Am Rand des Grundstückes soll ein Abstand von jeweils etwa 1,50m für einen Weg gelassen werden.
2.) Pro Weinrebe ergibt sich ein Ertrag von durchschnittlich 3 kg Trauben. (Erfahrungswert) Ein LKW kann maximal 5t transportieren. Wieviele ha Weinfelder lasse sich mit einem solchen LKW abtransportieren?
3.) Angenommen, die gesamte Ernte des 1ha Weinreben-Feldes passt auf einen LKW. Wieviele kg Trauben ergaben sich für diese Ernte pro Weinrebe durchschnittlich?
Lösungsideen: Zu 1.) Skizze machen, dann ergeben sich 98 x 98= 9604 Reben. Zu 2.) 9600 x 3kg = 28,8 t. Damit braucht es schon für 1 ha etwa 6 LKW-Fahrten. Zu 3.) 5000 kg: 9600 = ca. 0,5 kg - In der heissen Mittagspause bei Mendoza:
1.) 6 Freunde wollen 2 Melonen teilen. In wieviele Teile schneiden sie die Melonen am einfachsten? Gibt es mehrere Möglichkeiten?
2.) Emma backt Pfannkuchen. Für 10 Pfannkuchen braucht sie etwa 300 ml Milch. Die Packung hat 1,5l. Welcher Anteil ist nach dem Backen noch übrig, wenn sie vorher voll war? Wieviele Pfannkuchen könnte sie mit der ganzen Milch backen? (Wenn alle anderen Zutaten auch da sind!) - In Santiago im Park:
Anna möchte ein Sofa kaufen. Welches Sofa passt am Besten ins Zimmer? Wo würdest Du es hinstellen? (Es gibt verschiedene Möglichkeiten)
Sofa A : 0,7m x 2,2m Sofa B: 0,8m x 1,9m Sofa C: 0,7m x 2,0m
Mein Referendariat ist bereits seit einiger Zeit erfolgreich abgeschlossen, aber ich habe noch einige Dokumente, die ich gerne hier veröffentlichen möchte.
Im Rahmen meiner schriftlichen Examensarbeit hatte ich im Frühjahr im Rahmen des Mathematikunterrichtes einer 9.Klasse an der Stadtteilschule einen Ausflug in den Hamburger Hafen durchgeführt und dokumentiert.
Ziel des Unterrichtsversuches war, insbesondere die Stärkung der Bereitschaft, mathematische Erkundungen von realen Sachverhalten durchzuführen. Hierzu ist das Erkennen, Abschätzen und Modellieren von physikalischen und wirtschaftlichen Größen notwendig. Dies sollte und wurde durch einen deutlichen Bezug von mathematischen Herausforderungen auf ihren Kontext und damit in sinnstiftender Auseinandersetzung mit mathematischen Konzepten erreicht.
Titel meiner Hausarbeit war:
Inwieweit fördert die Beschäftigung mit mathematikhaltigen Herausforderungen im Kontext eines außerschulischen Lernortes Kompetenz und Bereitschaft, reale Situationen mit Hilfe mathematischer Mittel zu erkunden?
Eine Untersuchung in einer Klasse mit technischem Profil der Jahrgangsstufe 9 einer Hamburger Stadtteilschule am Beispiel des Hamburger Hafens
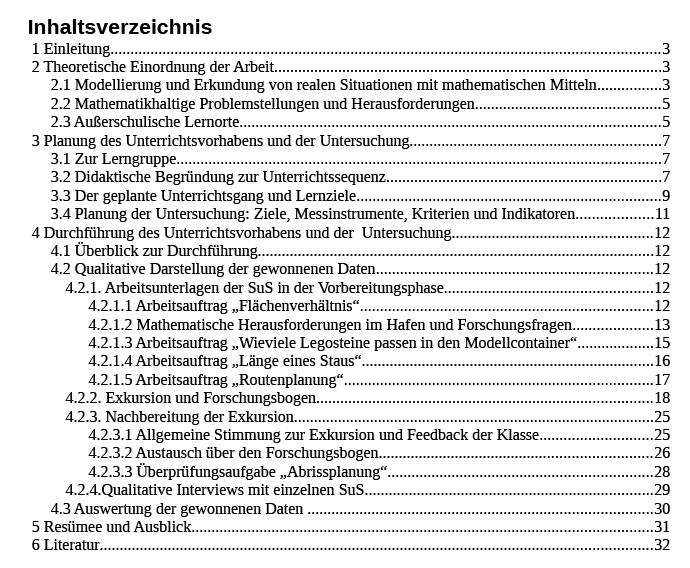
Da ich das gesamte Dokument noch einmal durchschauen möchte, bevor ich es gegebenenfalls online veröffentliche, stelle ich an dieser Stelle zunaechst nur das Inhaltsverzeichnis, die didaktischen Begruendungen und (zu einem spaeteren Zeitpunkt, da ich gerade nicht auf sie zugreifen kann) einige Arbeitsmaterialien zur Verfuegung. Fuer Fragen bin ich gerne per mail oder Kommentar auf dem Blog erreichbar.
3.2 Didaktische Begründung zur Unterrichtssequenz
Ich beziehe mich bei meinem Unterrichtsvorhaben sowohl auf den Bildungsplan für die Hamburger Stadtteilschulen in Mathematik (im weiteren BP-M) als auch auf den Bildungsplan für außerschulische Lernorte (im weiteren BP-AL).
Bei der Planung des Unterrichtsversuches war mir ein besonderes Anliegen, den SuS zu verdeutlichen, dass Mathematik, wie in Kapitel 2.2 erläutert, sich in verschiedenartigen Tätigkeitsfeldern bewährt hat und in Wechselwirkung mit diesen entstanden ist.
Mit einem übergreifenden thematischen Kontext für den Unterricht werden die Vorstellungen der SuS von den Möglichkeiten der Mathematik erweitert, die Vernetzung verschiedener Bereiche der Mathematik gefördert und angemessene Grundvorstellungen von Vorgehensweisen der Mathematik vermittelt. Zudem sollen Erfolgserlebnisse beim Lösen authentischer Probleme die Motivation der
SuS stärken, mathematische Mittel im Alltag zu verwenden.
Wie in Kapitel 2.1 beschrieben sollen Lerngegenstände immer an dem Vorwissen der Lernenden anknüpfen. Ich habe den Hamburger Hafen als Lerngegenstand gewählt, weil jeder Mensch in Hamburg ihn kennt und er wirtschaftlich eine hohe Relevanz für die Stadt hat. Zum Hafen lassen sich unterschiedlich komplexe mathematikhaltige Herausforderungen und Problemstellungen finden, die selbstdifferenzierendes Arbeiten ermöglichen. Durch die eindrucksvollen Mengen- und Größenverhältnisse wird hervorgehoben, wie wichtig mathematische Planung ist, die auch exemplarisch für andere Anwendungsbereiche ist.
Container als prägnante Objekte im Hafen sind durch ihre quaderförmige Form besonders geeignet, schwächeren SuS die Beschäftigung mit Volumina zu ermöglichen. Durch die große Anzahl der Container im Hamburger Hafen wird das Abschätzen von Größenverhältnissen und Mengen motiviert. Die geplanten Inhalte sind laut BP-M in der Unterstufe zu behandeln, allerdings sind sie in meiner Lerngruppe nicht abgesichert erlernt. Zudem bietet sich durch den Profilunterricht die Möglichkeit, zusätzliche Stunden zu nutzen, um das Forschungsumfeld ausreichend auszuleuchten und zu außermathematischen Themen im Kontext zu arbeiten. Ziel ist hierbei weniger die fachliche Berechnung zu beherrschen, als die Nützlichkeit in der Anwendung und die Modellierung der realen Situation zu betonen.
Der Bezug zur Lebenswirklichkeit der SuS ist durch das besondere technische Interesse gegeben; viele SuS streben eine technische Berufsausbildung an, wie es sie im Hafen in großem Umfang gibt. Einige Eltern arbeiten im Hafen bzw. in der Logistik; und so gut wie alle SuS haben den Hamburger Hafen bereits besucht, wenn auch zumeist nur mit Blick von den Landungsbrücken zum Eis essen.
Die Exkursion habe ich in Form einer Busfahrt im öffentlichen Nahverkehr, eines Besuches des Hafenmuseums und einer abschließenden Fährfahrt geplant. Die gemeinsame Anfahrt unterstreicht den Erlebnischarakter einer Exkursion, der, wie in Kapitel 2.3 geschildert, für das informelle Lernen relevant ist. Zusätzlich sind auf dem Weg beeindruckende Mengen an Containern und Hafenstrukturen zu erkennen. Im Hafenmuseum Hamburg sind viele Gerätschaften, Lagerbehälter und Schiffe sowie Kräne für Schulklassen kostenlos zu besichtigen und es sind Expertinnen und Experten anwesend.
Sowohl der öffentliche Nahverkehr als auch das Museum sind keine primären außerschulischen Lernorte in Bezug auf Mathematik, wie in Kapitel 2.3 dargestellt, sondern müssen von mir durch passendes Arbeitsmaterial und Einbettung dahingehend gestaltet werden. In der Fachliteratur zu Museumsbesuchen wird darauf hingewiesen, dass ein Lernzuwachs verstärkt wird „wenn das Lernen im Museum von gut strukturiertem Lernmaterial unterstützt wird.“21 Und im BP-AL: „Das Lernen vor Ort wird dann fruchtbar, wenn es mit einer Aufgabenstellung fokussiert wird, die zum forschenden und selbstgesteuerten Lernen anleitet. “22 Es gibt bereits didaktisch aufbereitetes
Material zum Hafenmuseum23, das ich auszugsweise für den fachlichen Kontext angereichert in einem Forschungsbogen verwenden werde. Die dort eingeforderten freien Formulierungen zu Vorgehensweisen ermöglichen eine Reflexion der SuS und sind diagnostisch für meine Untersuchung wichtig.
Museumsbesuche sind ungewöhnlich im Mathematikunterricht und das Hafenmuseum Hamburg nicht zu vergleichen mit dem Mathematikum in Giessen24 oder anderen mathematikdidaktisch gestalteten Einrichtungen. Es gibt aber im Hafenmuseum Möglichkeiten, mit wenig Aufwand mathematikhaltige Problemstellungen zu entdecken und zu bearbeiten.
Als Sozialform während des Museumsbesuches ist im wesentlichen das Arbeiten in Kleingruppen geplant. Gemeinsame Phasen wird es zu Beginn mit einem Experten des Hafenmuseums geben und zum Abschluss, um gemeinsam mit der Fähre zu fahren. Die Kleingruppen werden bereits in der Vorbereitungsphase an der Forschungsfrage gearbeitet haben. Das kooperative Arbeiten beim Museumsbesuch ermöglicht das Austauschen von Informationen und Meinungen, was neben der Förderung von Sozialkompetenzen auch das Erarbeiten der Lernangebote vor Ort fördert.
Um eine Tagesexkursion in den Hamburger Hafen ergiebig zu gestalten, wird der vor- und nachbereitende Unterrichtsgang für die SuS anspruchsvoller aber auch ergiebiger. Logistische und geographische Grundlagen sind von hoher Relevanz. Die Lösung realer oder realitätsnaher Fragestellungen mit mathematischen Mitteln ist, wie in Kapitel 2.1 beschrieben, anspruchsvoll.
Hierzu sagt der BP-M: „Die Schülerinnen und Schüler bearbeiten zunächst kleinere Beispiele, bei denen noch nicht der gesamte Modellierungskreislauf durchlaufen wird. “26 Zum Kennenlernen der Vorgehensweise lasse ich zunächst einfache realitätsbezogene Abschätzungen und Teilmodellierungen zu Längen, Flächen und Volumina vornehmen, die teilweise mehrere mögliche Lösungen haben, wie es in realen Situationen häufig der Fall ist. Durch das Lernen mit Material am Beispiel der Beladung eines Containers plane ich, durch enaktive Darstellungen alle SuS in der Auseinandersetzung mit Größenverhältnissen und Volumina von Quadern zu unterstützen.
Es sollen Herausforderungen im Kontext Hafen entdeckt werden und eine Forschungsfrage in Kleingruppen entwickelt werden, die gezielte Interpretation und Strukturierung von Daten erfordert, aber keine vollständige Modellierung. Dies soll die Bereitschaft zur Erkundung komplexer realer Situationen und das Zutrauen der SuS in ihre eigenen Kompetenzen fördern. Zum Einstieg wären
umfangreiche Modellierungen überfordernd.
Während des vor- und nachbereitenden Unterrichtes habe ich verschiedene Sozialformen und Aktionsformen gewählt. Geplant sind sowohl Einzelarbeit und stark gelenkte Phasen als auch forschende Recherchephasen und Erkundungen in Kleingruppen sowie Diskussionen in der
gesamten Lerngruppe. Für die Bearbeitung einer sehr offenen Problemstellung in reiner Forschungsform halte ich die Lerngruppe für nicht selbstständig genug und denke, es würde Überforderung und Enttäuschung eintreten. Die Nachbereitung soll neben einer emotionalen sowie fachlichen Auswertung der Exkursion auch einen Transfer beinhalten, der das Erlernte festigt.
Zur Differenzierung in der Lerngruppe, habe ich unter Berücksichtigung der in Kapitel 3.1 geschilderten Heterogenität Forschungsfragen mit Mindmap-Unterstützung vorgesehen sowie möglichst selbstdifferenzierende Aufgaben in Vor- und Nachbereitung entwickelt.
Nach einer längeren Pause aus verschiedenen Gründen setze ich mich nun daran, meinen Blog wieder mit aktuellen Informationen zu füttern.
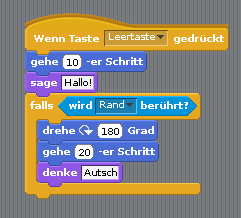
Seit einigen Wochen unterrichte ich einen Informatik-Wahlpflicht Kurs der 8.Klasse an einem Hamburger Gymnasium zum Thema „Software-Entwicklung“. Als erste Programmierumgebung nutzen wir Scratch, das als Programmiersprache eine Vielzahl an informatischen Konzepten einfach und visuell ansprechend umsetzt.
Nach einigen kleinen Übungen zur Entwicklungsumgebung und grundlegenden Anweisungs-Blöcken in Scratch sind wir nun in die umfangreichere Projektarbeit eingestiegen. Anhand einer technischen Problemstellung sollen die Schülerinnen und Schüler eigene Software-Lösungen entwickeln, überprüfen und erweitern.
Zur Problematisierung habe ich einen Videoclip gezeigt, der darstellt, wie das Löschen und der Weitertransport eines Containers im Hafen vonstatten geht.

Creative Commons: http://commons.wikimedia.org/wiki/File:MontrealExpress.jpg
Ziel der Projektarbeit ist, den Prozess des Van-Carriers, der die Container vom Kai am Schiff zum Zwischenlager transportiert, über eine Software zu automatisieren. Dies ist in einigen Containerterminals bereits der Fall, beispielsweise im Containerterminal Altenwerder. Herausfordernd ist hierbei neben der Steuerung eines Fahrzeuges auch der gesellschaftliche und arbeitstechnische Kontext, der typischerweise bei der Entwicklung von Software berücksichtigt werden sollte. Durch diese Einbettung in einen authentischen Kontext erwarte ich mir ein verstärktes Problembewusstsein, dass Software-Entwicklung mehr ist als Programmieren.
Hierfür wurde zunächst der Anwendungskontext untersucht und der wesentliche Arbeitsablauf herausgearbeitet, der automatisiert werden soll. Ein Arbeitsblatt sollte nach dem Video ausgefüllt werden und eine erste Modellierung des Prototypen ermöglichen:

Ein erster Plan als Modell für das Terminal
Als Kommunikations- und Dokumentationsmedium nutzen wir Blogs. Ich habe einen Lehrer-Blog, auf dem ich Aufgaben veröffentliche und Hilfestellungen gebe. Die Schülerinnen und Schüler haben ihren eigenen Blog, den sie vor allem als Lerntagebuch nutzen, aber auch zur Dokumentation ihrer Produkte.
Bisher läuft der Unterricht vielversprechend. Allerdings ist eine Doppelstunde pro Woche ziemlich wenig und den zuverlässigen Umgang mit einem Blog und ein angemessenes Lerntagebuch zu führen braucht Zeit und Übung. Aber besonders positiv ist für mich, dass ich direkte, individuelle Rückmeldungen bekomme und danach diagnostisch fördern und fordern kann.
Viele weitere hilfreiche Informationen zu Scratch gibt es hier:
Seit der letzten Woche behandel ich in der 8.Klasse das Thema „Grafen und Funktionen“. Den Einstieg habe ich mit einem Material aus mathematik lehren/ Heft 95 gestaltet mit der Zuordnung von Schulweg-Geschichten zu einfachen Grafen (siehe auch Regionale Lehrerfortbildung, Lernwerkstatt Mathematik „Unterrichtsbaustein Funktion“ S.40) Ergänzend habe ich für alle Schüler/innen, die zügig mit dieser Wiederholung zurecht kamen ein Arbeitsblatt aus mathematik lehren Heft 103/2000 zur Interpretation von verschiedenen Grafen und Situationen ausgeteilt. (siehe auch Regionale Lehrerfortbildung, Lernwerkstatt Mathematik „Unterrichtsbaustein Funktion“ S.22)
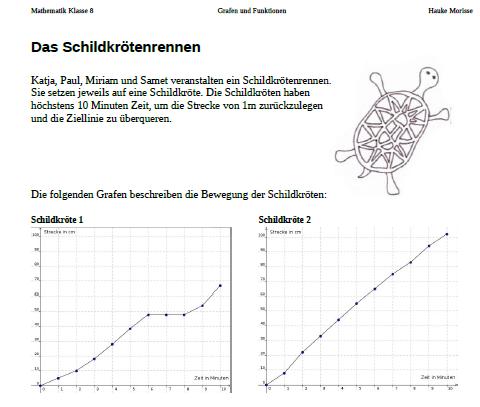
In der zweiten Stunde zum Thema habe ich ein umfangreicheres Szenario „Das Schildkrötenrennen“ problematisiert, dass ich angelehnt an die aktuelle Hauptschulprüfung in Hamburg entwickelt habe. (Informationen und Materialien sind hier: http://www.mint-hamburg.de/MA/ und hier: http://www.hamburg.de/startseite-hauptschulabschlusspruefung/)
Ich hatte als Problematisierung zum Einstieg in die Stunde das Thema vorgestellt und den geplanten Ablauf der Stunde angeschrieben. Dies nahm etwas zu viel Zeit in Anspruch, die sicher günstiger mit inhaltlichen Fragen gefüllt wäre als mit dem Anschreiben, aber gut war, dass Allen klar wurde, was auf sie zukommt. Zudem wurde mir bei der Reflexion mitgeteilt, dass der Aufhänger „Schildkrötenrennen“ inhaltlich ausführlicher ausgebreitet werden könnte, um die Schüler/innen tiefer in das inhaltliche Thema hineinzuversetzen. Nach dem Austeilen der Informationsblätter lies ich diese vorlesen und in eigenen Worten formulieren. Dies war insofern sinnvoll, dass den Schüler/innen auf verschiedenen Wegen das Szenario zugänglich gemacht wurde.
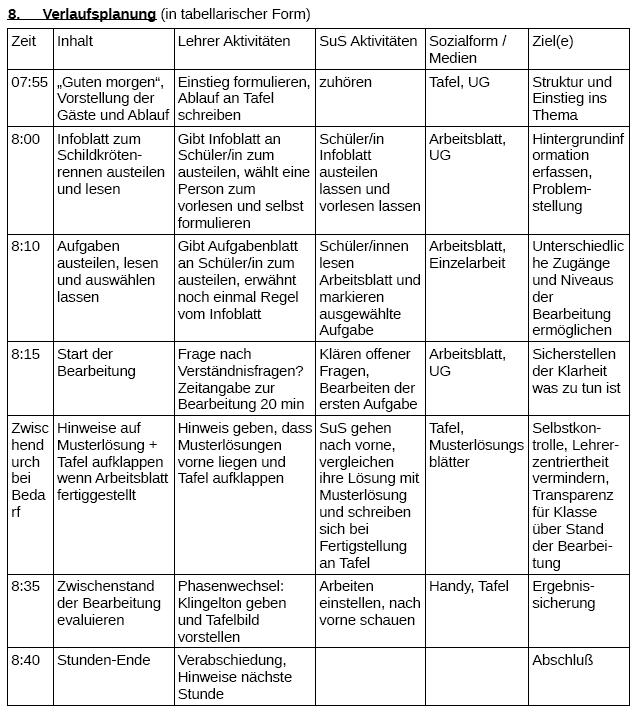
Die Aufgabenblätter habe ich bewusst danach seperat austeilen lassen, um die Schüler/innen nicht mit Material zu erschlagen und ihre Aufmerksamkeit schrittweise zu lenken. Dann kam die Bearbeitungsphase zu zweit, die ziemlich gut funktionierte. Allerdings wurden teilweise die vorne liegenden Musterlösungen ziemlich schnell herangezogen, möglicherweise auch nicht zur Selbstkontrolle, sondern zum Kopieren für die eigene Bearbeitung. Dies war ein erster Versuch in dieser Lerngruppe, mit Musterlösungen und Selbstkontrolle zu arbeiten und es hat noch nicht so geklappt, wie ich es vorgesehen hatte. Generell hatte diese Stunde viele neue Strukturmerkmale, dies sollte nach und nach angegangen werden und nicht so umfangreich auf einmal. In der Erarbeitungsphase gilt generell, sich vorher klar zu machen, was für eine Rolle ich als Lehrer spiele, also wie ich an welchen Stellen eingreife oder bewusst nicht eingreife. Die Menge und Übersichtlichkeit des Materials werde ich bei der Planung in Zukunft genauer aus Schüler/innen-Perspektive betrachten und dementsprechend prägnant und deutlicher strukturiert halten.
Die inhaltliche Sicherung am Ende werde ich stärker in die Planung mit einbeziehen. Die nachfolgende Stunde plane ich, noch detailierter auf Lösungen einzugehen, für diese Stunde hatte ich geplant, mit Musterlösungen und Kontrolle über die Tafel zu arbeiten, besser wäre sicher gewesen, einige wesentliche Inhalte noch einmal zu verbalisieren und zu visualisieren. Positiv war auf jeden Fall, dass sich Alle Schüler/innen auf ihren verschiedenen Niveaus differenziert mit der Interpretation von Grafen beschäftigt haben, was eines der wesentlichen Ziele der Stunde war.
Hier sind die Unterlagen (außer dem Unterrichtsentwurf, da dieser persönliche Daten und Details zu schulinternen Informationen beinhaltet):
Schildkroetenrennen – Materialien (zip – Datei)