In einer Fortbildung des Landesinstituts für Lehrerbildung in Hamburg zum Thema „interkulturelle Bildung“ haben wir uns an zwei Terminen mit verschiedenen Begriffen von „Kultur“ und Identitäten sowie der Sensibilisierung für einen transkulturellen Perspektivwechsel auseinandergesetzt.
Nach einer allgemeinen fachübergreifenden Einführung zu Identitäten und dem Umgang von Schule mit „Deutsch als Zweitsprache (DaZ)“ Schüler/innen beschäftigten wir uns handlungsorientiert mit Reaktionsmechanismen auf verschiedene „Regel“, um einen Umgang mit ungewohnten Verhaltensweisen durch eine sensibilisierte Sichtweise nachzuempfinden. Hierfür hatten wir ein Kartenspiel nach verschiedenen Regeln an verschiedenen Tischen gespielt ohne die Regeln explizit zu machen. Die Inhalte und Methoden bewegten den Blick weg vom „Problem mit den Schülern“ hin zum eigenen wertschätzenden Umgang mit „Fremdsein“ und dass nicht ohne Weiteres von sich auf andere geschlossen werden kann. Verschiedene Begrifflichkeiten und damit einhergehend Wertungen zu „Kultur“ wurden thematisiert und die Gespräche machten mir noch einmal deutlich, dass Erfahrungen mit „Fremdsein“ einigen Lehrer/innen durchaus fremd ist und wir als Lehrer/innen überwiegend weiß und bürgerlich mit Deutsch als erster Sprache behütet an Gymnasien sozialisiert wurden und somit systematisches Konfliktpotential in Schulen auftauchen muss. Dies einhergehend mit anderen gesellschaftlichen Rollen wie Gender, soziale Herkunft / Klasse und anderen Fremd- und Eigen-Identitätszuschreibungen erzeugt ein sehr komplexes Bild von sozialen Beziehungen in und um Schule.
Interessant fand ich bei der Beschäftigung mit den fachspezifischen didaktischen Überlegungen mit „transkultureller Brille“ (denn schließlich geht es weniger um Interkulturalität, also zwischen Kulturen arbeiten, sondern um die Einübung einer kulturübergreifenden und flexiblen Sichtweise auf kulturelle Praxen) die geringe Ausprägung dieser Sichtweise im Fach Mathematik. Sicherlich scheint Sprachunterricht zunächst naheliegender für eine transkulturelle Sichtweise zu sein, da Sprachförderung zur „Problembehebung“ mit DaZ Schüler/innen allgemein zum Standardprogramm gehört. Auf der anderen Seite erscheint gerade die Formalität und Fachsprache im Mathematik-Unterricht gerade für diese Schüler/inne mit DaZ eine Hürde darzustellen, die auf den Mangel an transkultureller Sichtweise in diesem Feld zurückzuführen ist. Wie in anderen Fächern auch gibt es eine doppelte Herausforderung für diese Schüler/innen, die Fachliche und die Sprachliche. Die Frage, die sich stellt, ist ob diesen Schüler/innen mit mehr Textarbeit und Sprachübungen im Mathematik-Unterricht geholfen ist oder mit bewusster Reduzierung der Fachsprache, um motivierende Erfolgserlebnisse zumindest auf mathematischer Ebenen zu ermöglichen. Ich denke wie häufig im pädagogischen Bereich gibt es nicht eine Antwort, sondern ein mehr oder weniger angemessenes Mischungsverhältnis. Insbesondere ist hierbei wichtig, die Unterrichtsvorbereitung und -nachbereitung immer wieder auch einmal durch eine „transkulturelle Brille“ zu reflektieren.
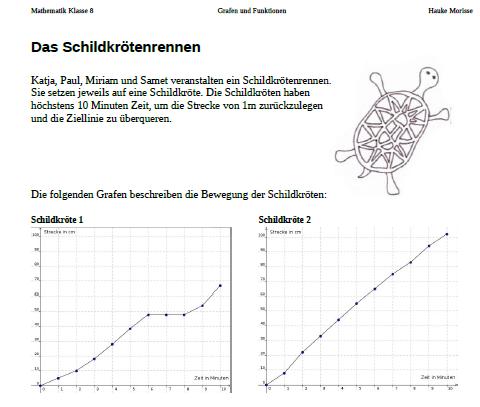
In unserer Kleingruppen-Arbeit zu Mathematik und transkultureller Bildung diskutierten wir eher über Zugänge zu mathematischen Konzepten allgemein, auch weil wir uns vorher in dieser Konstellation noch nie über didaktische Fragestellungen ausgetauscht hatten. Eines unserer Themen war: „Minus mal Minus gibt Plus“, wie kann das in den Horizont der Kinder gerückt werden? Ein weiteres Thema waren tragfähige Grundvorstellungen und Zugänge zu mathematischen Konzepten über verschiedene Strukturen wie grafische und ikonische Darstellungen und Arbeitsformen. Es wurde in Bezug auf andere Kulturkreise diskutiert, inwieweit Teamgeist und Kooperation in Kleingruppenarbeit stärker ausgeprägt seien und dies für den Unterricht nutzbar sei. Dann diskutierten wir über Aktivierung und Rollen in Gruppenarbeitsphasen sowie Anreize durch positive Verstärkung. Abschließend sprachen wir über Sprache und Mathematik-Unterricht. Mit einer transkulturellen Sichtweise kann in zwei Richtungen argumentiert werden, entweder die verstärkte Verwendung einfacher Sprache im Mathematikunterricht, um das Sprechen über Mathematik zu fördern und zu erleichtern oder entgegengesetzt die Verwendung von Sprache allgemein zu reduzieren, um die Doppelbelastung im Lernprozess zu reduzieren und auf die mathematischen Konzepte zu fokussieren. Viele Schüler/innen mit Deutsch als Zweitsprache haben Schwierigkeiten mit Formulierungen von Aufgaben. Dies lässt sich nach meiner Erfahrung im Sinne einer inklusiven Sichtweise noch weiter verschärfen darauf, dass allgemein auch Schüler/innen mit Deutsch als erster Sprache, die sprachliche Schwierigkeiten haben gleiche Doppelbelastungen erfahren.
In der Fachliteratur finden sich teilweise interessante Ansätze, die gerade die (mathematische) Sprachförderung ins Zentrum stellen, so beispielsweise das Arbeitsbuch „DaZ im Fachunterricht: Mathematik – Statistik für Anfänger“ (1). Auf der anderen Seite finden sich auch Aufgabentypen und inhaltliche Ansätze, die nach erster Sicht eher auf eigene Rassismen und Sensibilisierungen hinterfragt werden sollten. Wenn in Themenheften zu Mathematik und Interkulturalität neben „Tonleitern der Weltkulturen“ und „Kalenderberechnungen“ nur „Intelligenzvergleiche“, „Über- und Unterentwicklung“ und „Kriminalitätsraten“ als Titel auftauchen, darf man sich Sorgen machen, selbst wenn die Themen kritisch aufbereitet werden (was ich nur bedingt beurteilen kann, da ich sie nicht vollständig gesichtet habe, zudem ist einer der Artikel 11 Jahre alt). Da stellt sich die Frage, was für ein Bild von anderen Kulturen in Deutschland vorherrscht. Vergleiche (3) und (4)
Sinnvoll finde ich die folgende inhaltliche Bestimmungen auf der abstrakteren Ebene: „Im Mathematikunterricht kann die Vielfalt kultureller Wurzeln der eigenen Rechenkultur veranschaulicht, die Zahlensymbolik als Ausdruck bestimmter Weltdeutung behandelt oder bei Beispielaufgaben kulturelle Vielfalt repräsentiert werden.“ (http://www.bildungsserver.de/Mathematik-3383.html)
Das Buch „Zahlenwelten“ (2) hat ein ähnliches Mischungsverhältnis von Inhalten, die aus heutiger Sicht eher problematisch bis kontraproduktiv wirken, als auch Ansätze, die ich gerne ausprobieren möchte. Mathematisch logische Spiele aus anderen Kulturkreisen wie Patolli im Unterricht zu verwenden hat eben einen solchen wertschätzenden Bezug zu anderen Kulturen. Andererseits wird auch angeregt, statistisch „Ausländer an unserer Schule“ zu erheben und Berechnungen zu Unterkünften für Flüchtlinge anzustellen, die sicher kritisch begleitet Einsichten ermöglichen in gesellschaftliche Problemfelder, aber ebenso verstanden werden können, wie oben bereits benannt, dass andere Kulturen oder Kinder mit DaZ immer im negativen Kontext erwähnt werden oder als „das Andere“ dargestellt werden, statt ins Zentrum zu rücken, dass es kein „normal“ und „anders“ gibt, sondern alle Menschen in gewissen Kontexten als „normal“ gelten und in anderen als „anders“.
Zu unterscheiden bleibt das „strukturelle Mitdenken“ von transkultureller Bildung, z.B. durch Sprachwahl und Darstellungsarten und „inhaltliche Wandlung“ z.B. in Form vom wertschätzendem Aufgreifen verschiedener kulturell-historischer Wurzeln der Mathematik als Thema im Unterricht oder auch problemorientierte Beispiele, die nicht auf Fragestellungen aus dem Deutschen oder Europäischen Raum begrenzt bleiben.
Zum ersten Ansatz ist folgende Betrachtung hilfreich: „Betrachtet man das Spektrum schulischer Fächer genauer, so stellt sich heraus, dass es in allen Fächern kulturelle und fachgeschichtliche Prämissen und Traditionen gibt, die sich bei einer „interkulturellen Revision“ – mal mehr, mal weniger – als sperrig erweisen.“ (3) Beim zweiten Ansatz ist immer auch die Hinterfragung der eigenen Position als wohlmöglich Weißer Europäer mit Deutsch als Erstsprache unabdingbar, ist doch schnell aus gutem Vorhaben ein schräges Bild geworden, in dem es nicht um eine transkulturell reflektierte selbstbestimmte Identität der Schüler/innen, sondern um Zuschreibungen mit einhergehenden Wertungen von außen geht. Hier sollte nach meiner Einschätzung die Schüler/innen-Zentrierung in der Methodik besonders stark gemacht werden.
Literatur zum Thema:
(1) Nina Bödeker Olaf Gent: „DaZ im Fachunterricht: Mathematik – Statistik für Anfänger“ 5./6. Klasse, Persen Verlag 2010 (http://buecher-de.welt.de/shop/deutsch-als-fremdsprache/mathematik-statistik-fuer-anfaenger/boedeker-nina-gent-olaf/products_products/detail/prod_id/30530497/)
(2) Joachim Schroeder: „Zahlen-Welten: Bausteine für einen interkulturellen Mathematikunterricht“ Armin Vaas Verlag, 1994 (http://www.buchpreis-suche.de/zahlen-welten-bausteine-f%C3%BCr-einen-interkulturellen-mathematikunterricht.htm)
(3) Mathematik-Unterrichts-Einheiten-Datei e.V. „interkulturelles Lernen„: http://www.mued.de/html/inhalte/i3-multikulti.html
(4) Handreichung: Impulse für das interkulturelle Lernen Forum 1 / 2001, UNESCO Projekt Schulen http://www.ups-schulen.de/forum/01-1/forum-27-37.pdf
(5) S.Prediger: „Mathematiklernen als interkulturelles Lernen – Entwurf für einen didaktischen Ansatz„, in: Journal für Mathematikdidaktik 22 (2001) (http://www.mathematik.uni-dortmund.de/~prediger/veroeff/01-jmd-ml-as-ik.html)