Seacloud in der Oberstufe

 Auslandsschule, Lernwerkzeuge, Mathematik-Unterricht  No Responses »
Okt 172014
 

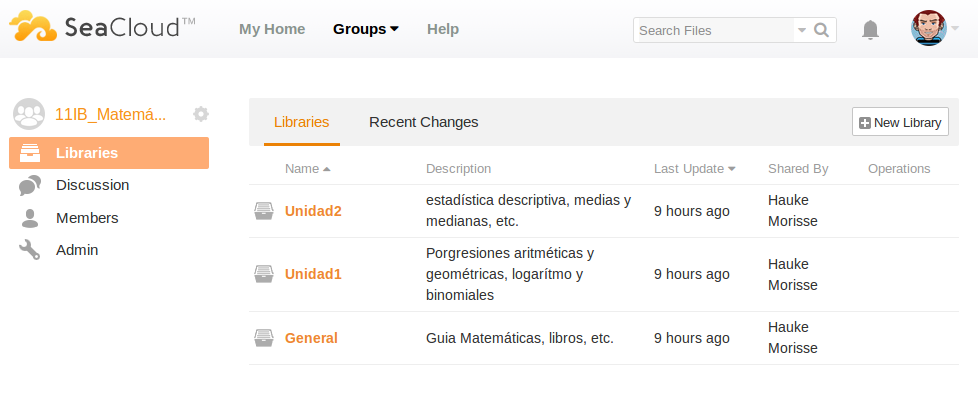
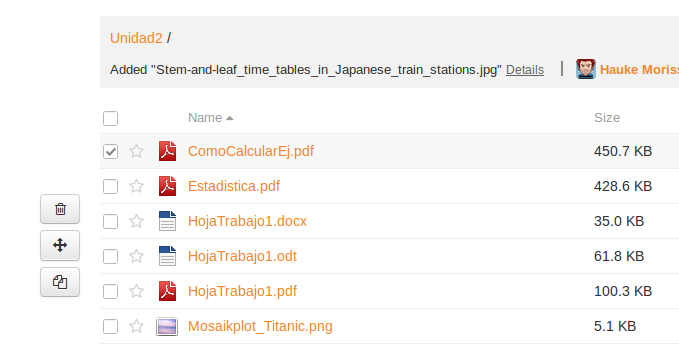
Ab heute arbeiten wir im Mathe-Unterricht mit der offenen Plattform seacloud.cc. Thematisch steigen wir nun in die deskriptive Statistik ein. Aufmerksam geworden bin ich auf diese einfache und effektive Lösung zur digitalen „Materialverwaltung“ durch einen Kollegen an meiner Schule, der in seinem Fachunterricht in der gleichen Klasse ebenfalls Seacloud benutzt. Einfach zu handhaben, hier ein paar erste Eindrücke:

Jede Gruppe hat ihre Bibliotheken und Diskussionen

Jede Gruppe hat ihre Bibliotheken und Diskussionen

Als nöchstes probiere ich dann aus, digitale Arbeitsblattvorlagen zu verteilen und diese bearbeitet digital abgeben zu lassen

Als nöchstes probiere ich dann aus, digitale Arbeitsblattvorlagen zu verteilen und diese bearbeitet digital abgeben zu lassen

[Mathe-Unterricht] IB Kurs 11 – erste Unterrichtsstunden auf Spanisch

 Auslandsschule, Mathematik-Unterricht  No Responses »
Sep 282014
 

Nach weniger als einem Monat bin ich in meiner 11.Klasse des IB-Kurses bereits fast am Ende der ersten Unterrichtseinheit zu den Themen „arithmetische und geometrische Reihen, Binomialentwicklung sowie Potenzen und Logarithmen“ Wir arbeiten mit dem Buch „Mathematics for the international student“ in englischer Sprache, gelegentlich streue ich auch deutschsprachiges oder spanischsprachiges Material ein. Die Unterrichtssprache ist Spanisch. Das macht insofern Sinn, dass auch die Abschlussprüfungen auf Spanisch sein werden und die SuS, fast ausschliesslich muttersprachlich spanisch, damit entlastet werden. Auf der anderen Seite haben alle SuS im IB-Kurs verpflichtend Deutsch und Englisch auf hohem Niveau, so dass ich gelegentlich vom Spanischen abweichen kann. Für mich ist es das erste mal, das ich nicht auf Deutsch unterrichte, aber es funktioniert ganz gut und ich kann mir kaum eine bessere Form vorstellen, Sprachkenntnisse zu verbessern, als durch eigenen Unterricht.

Haptische Mathematik mit dem Turm von Hanoi

Haptische Mathematik mit den Türmen von Hanoi

Zu dem Diploma-Programm des IB gibt es sehr viele Ressourcen, aber diese sind rechtlich geschützt, so dass ich den Grossteil meiner Arbeitsunterlagen hier im Blog nicht veröffentlichen werde. Viele der Unterlagen lassen sich bei der IBO direkt erwerben. Die Questionbank-Aufgaben beispielsweise geben einen guten Eindruck, welche inhaltlichen und formalen Schwerpunkte der jeweilige Prüfungsteil hat.

Ein Punkt entspricht etwa einer Minute Bearbeitungszeit.

Ein Punkt entspricht etwa einer Minute Bearbeitungszeit, Auszug aus der Questionbank „Series and Aplications“.

Es gibt auch eine eigene Formelsammlung, die uns von der IBO zur Verfügung gestellt wird, die zu jeder Unterrichtseinheit die wesentlichen Formeln enthält und bei Prüfungen als Arbeitshilfe zugelassen ist.

Auszug aus dem Cuadernillo / Formelsammlung zur Unidad 1

Auszug aus dem Cuadernillo / Formelsammlung zur Unidad 1

Gerade zum Einstieg in einen Themenbereich bieten sich praktische Problemstellungen an. So habe ich zur Einleitung der geometrischen Folge das Beispiel „Tschernobyl“ und die Berechnung eines radioaktiven Zerfalles genutzt, um anschließend mithilfe des Logarithmus die Halbwertzeit zu bestimmen. Die Idee stammt aus einem der deutschsprachigen Mathebücher unserer Bibilothek. Die Verbindung zur historischen Entwicklung bietet ebenfalls Stoff für die Problemorientierung, beispielsweise mit den Paradoxien von Zenon, den Türmen von Hanoi oder die Legende von den Weizenkörnern auf dem Schachbrett zu exponentiellem Wachstum. Zur Berechnung des Zinseszins sind geometrische Folgen ebenfalls geeignet und das Pascalsche Dreieck bietet einen Überblick zur Binomialentwicklung. Allerdings brauchen wir auch viel Zeit zum Einüben der formalen Schreibweisen und Berechnungen und das Arbeitstempo ist hoch.

Eine der Paradoxien von Zenon: Achilles und die Schildkröte

Das IB-Programm für den Mathematik-Kurs (SL) umfasst folgende Bereiche im Zeitraum von zwei Jahren:

  • Unidad 1: Álgebra
  • Unidad 2: Funciones y ecuaciones
  • Unidad 3: Funciones circulares y trigonometría
  • Unidad 4: Vectores
  • Unidad 5: Estadística y probabilidad
  • Unidad 6: Análisis
  • Exploración matemática

Viele Themen sind dem deutschen Abitur sehr ähnlich, allerdings ist die Stoffmenge, Verknüpfung mit anderen Fächern, beispielsweise „Theory of Knowledge“ und Form der (externen) Prüfungen nach meiner erster Einschätzung umfangreicher. Wir unterrichten Mathematik grundsätzlich 5-Stündig in der 11. und 12. Klasse und die SuS haben fast jeden Tag auch Nachmittagsunterricht. Die „Exploración matematica“ ist eine Art verbindliche Facharbeit, die über 6 bis 12 Seiten zu einem selbstgewählten Thema frei erarbeitet wird und einen Anteil an der abschliessenden Bewertungsgrundlage liefert. Es gibt zahlreiche Raster zu Qualitätsmerkmalen und Bewertungsgrundlagen dieser Ausarbeitung, die den SuS zur Verfügung gestellt werden. Auch das verpflichtende Essay über 4.000 Wörter kann im Fach Mathematik geschrieben werden. Einige Arbeitsunterlagen habe ich ergänzend zum Buch, den Questionbank-Aufgaben und Materialien von Kolleg/innen auch selbst erstellt, die ich hiermit zur Verfügung stelle:

Kleine Mathematik-Überlegungen auf Reisen

 Mathematik-Unterricht  No Responses »
Aug 252014
 

Während der letzten Monate und besonders nun, wenige Tage vor Schulbeginn habe ich mir immer mal wieder Gedanken zu kleinen Mathematik-Projekten oder -Aufgaben gemacht, die ich hier vorstellen möchte. Es geht gar nicht um besonders innovative Konzepte, sondern eher spontane Überlegungen, an denen ich getüftelt hatte. Dabei war mir weniger die konkrete Ausgestaltung wichtig, als Impulse festzuhalten.

  • Irgendwo unterwegs: Aus Temperaturtdiagrammen einer frei wählbaren Stadt der Welt (z.B. über Smartphones/Internetbrowser oder Lehrerrecherche) eine Tabelle erstellen und umgedreht, danach vergleichen und evt. über Wahl der Städte sprechen. Ziel dieser Aufgabe ist, Gesprächsanlässe und positive Bezugnahme auf Migrationshintergründe auch im Mathematikunterricht zu geben.
  • bei Mendoza, Argentinien im Weinanbau-Gebiet:
    1.) Weinreben werden etwa in einem Abstand von 1m voneinander gepflanzt. Wieviele Reben passen etwa auf 1 ha Land? (1ha = 100m x 100m)
    Am Rand des Grundstückes soll ein Abstand von jeweils etwa 1,50m für einen Weg gelassen werden.
    2.) Pro Weinrebe ergibt sich ein Ertrag von durchschnittlich 3 kg Trauben. (Erfahrungswert) Ein LKW kann maximal 5t transportieren. Wieviele ha Weinfelder lasse sich mit einem solchen LKW abtransportieren?
    3.) Angenommen, die gesamte Ernte des 1ha Weinreben-Feldes passt auf einen LKW. Wieviele kg Trauben ergaben sich für diese Ernte pro Weinrebe durchschnittlich?
    Lösungsideen: Zu 1.) Skizze machen, dann ergeben sich 98 x 98= 9604 Reben. Zu 2.) 9600 x 3kg = 28,8 t. Damit braucht es schon für 1 ha etwa 6 LKW-Fahrten. Zu 3.) 5000 kg: 9600 = ca. 0,5 kg
  • In der heissen Mittagspause bei Mendoza:
    1.) 6 Freunde wollen 2 Melonen teilen. In wieviele Teile schneiden sie die Melonen am einfachsten? Gibt es mehrere Möglichkeiten?
    2.) Emma backt Pfannkuchen. Für 10 Pfannkuchen braucht sie etwa 300 ml Milch. Die Packung hat 1,5l. Welcher Anteil ist nach dem Backen noch übrig, wenn sie vorher voll war? Wieviele Pfannkuchen könnte sie mit der ganzen Milch backen? (Wenn alle anderen Zutaten auch da sind!)
  • In Santiago im Park:
    Anna möchte ein Sofa kaufen. Welches Sofa passt am Besten ins Zimmer? Wo würdest Du es hinstellen? (Es gibt verschiedene Möglichkeiten)
    Sofa A : 0,7m x 2,2m        Sofa B: 0,8m x 1,9m     Sofa C: 0,7m x 2,0m

Projektorientierter Unterricht – muendliche Pruefung Referendariat

 Informatik-Unterricht, Mathematik-Unterricht, Referendariat, Schule allgemein  1 Response »
Okt 272013
 

Wie bereits im letzten Beitrag geschrieben ist das Referendariat nun einige Zeit her, aber besonders fuer diejenigen, denen eine muendliche Pruefung noch bevorsteht, moechte ich hier etwas zu dieser schreiben und meine Unterlagen zur Verfuegung stellen.

Als uebergreifenden Aufhaenger habe ich mir die effektive individuelle Foerderung durch projektorientierten Unterricht und Diagnose fuer die Pruefung ueberlegt. Dies hatte zum einen den Vorteil, das ich in diesem Bereich einige Erfahrungen im Referendariat sammeln konnte und diese aufbereitet darstellen konnte, zum anderen, dass mich projektorientierte Arbeitsweisen ueberzeugen und ich die theoretischen Ueberlegungen zur Entwicklung von Unterrichtsqualitaet interessant finde. Daher hatte ich mir auch als aktuelle Lektuere die Erhebungen von Hattie zugrundegelegt, aber auch Klassiker des Projekt(orientierten) Unterrichtes u.a. von Johannes Bastian. Das Pruefungsgespraech unterstuetzte ich mit farbigen Karten an einer Pinnwand, die in ihrer Struktur dem Handout entsprachen und mir gleichzeitig als Unterstuetzung im Redefluss dienten. Die Pruefung verlief sehr gut und es ergaben sich interessante Diskussionen besonders ueber Potentiale und Grenzen der Projektmethoden.

Hier meine Handouts:

´Wie muss projektorientierter Unterrricht strukturiert sein, um zielorientiert und erfolgreich zu sein?` (Allgemeindidaktik)

´Klassenführung im projektorientierten Unterricht der Mittelstufe: Wie kann die durchgeführte Unterrichtseinheit „Robotik WP-7“ für die Zukunft optimiert werden?´ (Informatik)

 ´Wie kann Diagnose im Spannungsfeld der Lehrerrollen Prüfer und Berater insbesondere in der Vorstufe einer Stadtteilschule gelingen?´ (Mathematik)

[Mathe-Unterricht] Außerschulischer Lernort Hamburger Hafen

 Mathematik-Unterricht, Projektarbeit u Exkursionen, Referendariat  3 Responses »
Okt 252013
 

Mein Referendariat ist bereits seit einiger Zeit erfolgreich abgeschlossen, aber ich habe noch einige Dokumente, die ich gerne hier veröffentlichen möchte.

Im Rahmen meiner schriftlichen Examensarbeit hatte ich im Frühjahr im Rahmen des Mathematikunterrichtes einer 9.Klasse an der Stadtteilschule einen Ausflug in den Hamburger Hafen durchgeführt und dokumentiert.

Ziel des Unterrichtsversuches war, insbesondere die Stärkung der Bereitschaft, mathematische Erkundungen von realen Sachverhalten durchzuführen. Hierzu ist das Erkennen, Abschätzen und Modellieren von physikalischen und wirtschaftlichen Größen notwendig. Dies sollte und wurde durch einen deutlichen Bezug von mathematischen Herausforderungen auf ihren Kontext und damit in sinnstiftender Auseinandersetzung mit mathematischen Konzepten erreicht.

Titel meiner Hausarbeit war:

Inwieweit fördert die Beschäftigung mit mathematikhaltigen Herausforderungen im Kontext eines außerschulischen Lernortes Kompetenz und Bereitschaft, reale Situationen mit Hilfe mathematischer Mittel zu erkunden?
Eine Untersuchung in einer Klasse mit technischem Profil der Jahrgangsstufe 9 einer Hamburger Stadtteilschule am Beispiel des Hamburger Hafens

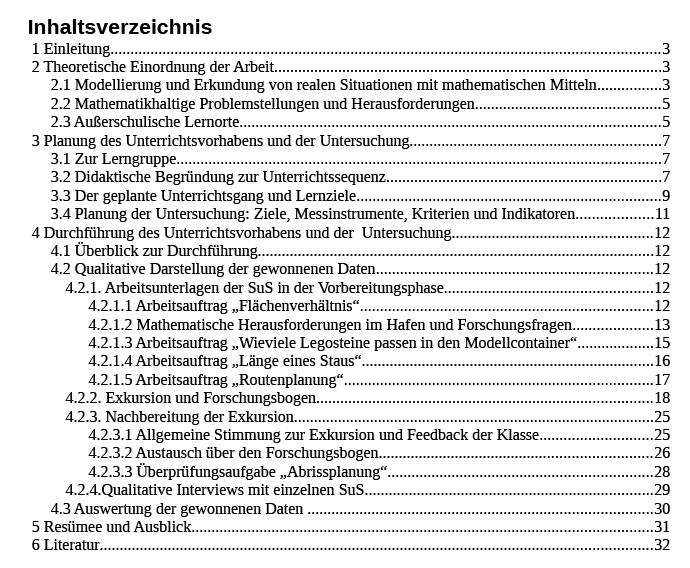
Da ich das gesamte Dokument noch einmal durchschauen möchte, bevor ich es gegebenenfalls online veröffentliche, stelle ich an dieser  Stelle zunaechst nur das Inhaltsverzeichnis, die didaktischen Begruendungen und (zu einem spaeteren Zeitpunkt, da ich gerade nicht auf sie zugreifen kann) einige Arbeitsmaterialien zur Verfuegung. Fuer Fragen bin ich gerne per mail oder Kommentar auf dem Blog erreichbar.

3.2 Didaktische Begründung zur Unterrichtssequenz

Ich beziehe mich bei meinem Unterrichtsvorhaben sowohl auf den Bildungsplan für die Hamburger Stadtteilschulen in Mathematik (im weiteren BP-M) als auch auf den Bildungsplan für außerschulische Lernorte (im weiteren BP-AL).
Bei der Planung des Unterrichtsversuches war mir ein besonderes Anliegen, den SuS zu verdeutlichen, dass Mathematik, wie in Kapitel 2.2 erläutert, sich in verschiedenartigen Tätigkeitsfeldern bewährt hat und in Wechselwirkung mit diesen entstanden ist.
Mit einem übergreifenden thematischen Kontext für den Unterricht werden die Vorstellungen der SuS von den Möglichkeiten der Mathematik erweitert, die Vernetzung verschiedener Bereiche der Mathematik gefördert und angemessene Grundvorstellungen von Vorgehensweisen der Mathematik vermittelt. Zudem sollen Erfolgserlebnisse beim Lösen authentischer Probleme die Motivation der
SuS stärken, mathematische Mittel im Alltag zu verwenden.
Wie in Kapitel 2.1 beschrieben sollen Lerngegenstände immer an dem Vorwissen der Lernenden anknüpfen. Ich habe den Hamburger Hafen als Lerngegenstand gewählt, weil jeder Mensch in Hamburg ihn kennt und er wirtschaftlich eine hohe Relevanz für die Stadt hat. Zum Hafen lassen sich unterschiedlich komplexe mathematikhaltige Herausforderungen und Problemstellungen finden, die selbstdifferenzierendes Arbeiten ermöglichen. Durch die eindrucksvollen Mengen- und Größenverhältnisse wird hervorgehoben, wie wichtig mathematische Planung ist, die auch exemplarisch für andere Anwendungsbereiche ist.

Container als prägnante Objekte im Hafen sind durch ihre quaderförmige Form besonders geeignet, schwächeren SuS die Beschäftigung mit Volumina zu ermöglichen. Durch die große Anzahl der Container im Hamburger Hafen wird das Abschätzen von Größenverhältnissen und Mengen motiviert. Die geplanten Inhalte sind laut BP-M in der Unterstufe zu behandeln, allerdings sind sie in meiner Lerngruppe nicht abgesichert erlernt. Zudem bietet sich durch den Profilunterricht die Möglichkeit, zusätzliche Stunden zu nutzen, um das Forschungsumfeld ausreichend auszuleuchten und zu außermathematischen Themen im Kontext zu arbeiten. Ziel ist hierbei weniger die fachliche Berechnung zu beherrschen, als die Nützlichkeit in der Anwendung und die Modellierung der realen Situation zu betonen.

Der Bezug zur Lebenswirklichkeit der SuS ist durch das besondere technische Interesse gegeben; viele SuS streben eine technische Berufsausbildung an, wie es sie im Hafen in großem Umfang gibt. Einige Eltern arbeiten im Hafen bzw. in der Logistik; und so gut wie alle SuS haben den Hamburger Hafen bereits besucht, wenn auch zumeist nur mit Blick von den Landungsbrücken zum Eis essen.
Die Exkursion habe ich in Form einer Busfahrt im öffentlichen Nahverkehr, eines Besuches des Hafenmuseums und einer abschließenden Fährfahrt geplant. Die gemeinsame Anfahrt unterstreicht den Erlebnischarakter einer Exkursion, der, wie in Kapitel 2.3 geschildert, für das informelle Lernen relevant ist. Zusätzlich sind auf dem Weg beeindruckende Mengen an Containern und Hafenstrukturen zu erkennen. Im Hafenmuseum Hamburg sind viele Gerätschaften, Lagerbehälter und Schiffe sowie Kräne für Schulklassen kostenlos zu besichtigen und es sind Expertinnen und Experten anwesend.

Sowohl der öffentliche Nahverkehr als auch das Museum sind keine primären außerschulischen Lernorte in Bezug auf Mathematik, wie in Kapitel 2.3 dargestellt, sondern müssen von mir durch passendes Arbeitsmaterial und Einbettung dahingehend gestaltet werden. In der Fachliteratur zu Museumsbesuchen wird darauf hingewiesen, dass ein Lernzuwachs verstärkt wird „wenn das Lernen im Museum von gut strukturiertem Lernmaterial unterstützt wird.“21 Und im BP-AL: „Das Lernen vor Ort wird dann fruchtbar, wenn es mit einer Aufgabenstellung fokussiert wird, die zum forschenden und selbstgesteuerten Lernen anleitet. “22 Es gibt bereits didaktisch aufbereitetes
Material zum Hafenmuseum23, das ich auszugsweise für den fachlichen Kontext angereichert in einem Forschungsbogen verwenden werde. Die dort eingeforderten freien Formulierungen zu Vorgehensweisen ermöglichen eine Reflexion der SuS und sind diagnostisch für meine Untersuchung wichtig.

Museumsbesuche sind ungewöhnlich im Mathematikunterricht und das Hafenmuseum Hamburg nicht zu vergleichen mit dem Mathematikum in Giessen24 oder anderen mathematikdidaktisch gestalteten Einrichtungen. Es gibt aber im Hafenmuseum Möglichkeiten, mit wenig Aufwand mathematikhaltige Problemstellungen zu entdecken und zu bearbeiten.

Als Sozialform während des Museumsbesuches ist im wesentlichen das Arbeiten in Kleingruppen geplant. Gemeinsame Phasen wird es zu Beginn mit einem Experten des Hafenmuseums geben und zum Abschluss, um gemeinsam mit der Fähre zu fahren. Die Kleingruppen werden bereits in der Vorbereitungsphase an der Forschungsfrage gearbeitet haben. Das kooperative Arbeiten beim Museumsbesuch ermöglicht das Austauschen von Informationen und Meinungen, was neben der Förderung von Sozialkompetenzen auch das Erarbeiten der Lernangebote vor Ort fördert.

Um eine Tagesexkursion in den Hamburger Hafen ergiebig zu gestalten, wird der vor- und nachbereitende Unterrichtsgang für die SuS anspruchsvoller aber auch ergiebiger. Logistische und geographische Grundlagen sind von hoher Relevanz. Die Lösung realer oder realitätsnaher Fragestellungen mit mathematischen Mitteln ist, wie in Kapitel 2.1 beschrieben, anspruchsvoll.
Hierzu sagt der BP-M: „Die Schülerinnen und Schüler bearbeiten zunächst kleinere Beispiele, bei denen noch nicht der gesamte Modellierungskreislauf durchlaufen wird. “26 Zum Kennenlernen der Vorgehensweise lasse ich zunächst einfache realitätsbezogene Abschätzungen und Teilmodellierungen zu Längen, Flächen und Volumina vornehmen, die teilweise mehrere mögliche Lösungen haben, wie es in realen Situationen häufig der Fall ist. Durch das Lernen mit Material am Beispiel der Beladung eines Containers plane ich, durch enaktive Darstellungen alle SuS in der Auseinandersetzung mit Größenverhältnissen und Volumina von Quadern zu unterstützen.

Es sollen Herausforderungen im Kontext Hafen entdeckt werden und eine Forschungsfrage in Kleingruppen entwickelt werden, die gezielte Interpretation und Strukturierung von Daten erfordert, aber keine vollständige Modellierung. Dies soll die Bereitschaft zur Erkundung komplexer realer Situationen und das Zutrauen der SuS in ihre eigenen Kompetenzen fördern. Zum Einstieg wären
umfangreiche Modellierungen überfordernd.

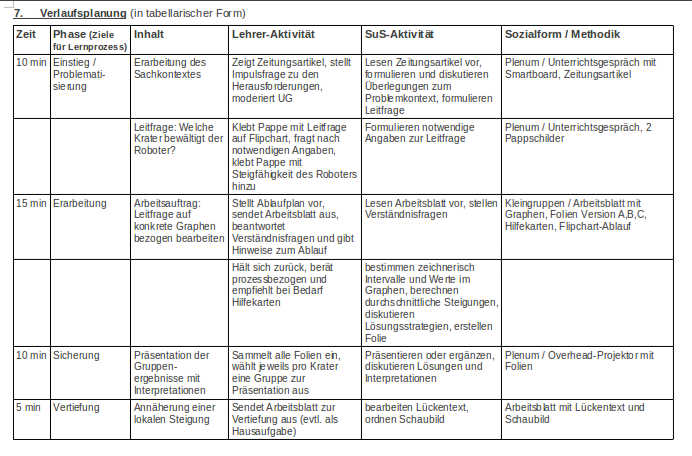
Während des vor- und nachbereitenden Unterrichtes habe ich verschiedene Sozialformen und Aktionsformen gewählt. Geplant sind sowohl Einzelarbeit und stark gelenkte Phasen als auch forschende Recherchephasen und Erkundungen in Kleingruppen sowie Diskussionen in der
gesamten Lerngruppe. Für die Bearbeitung einer sehr offenen Problemstellung in reiner Forschungsform halte ich die Lerngruppe für nicht selbstständig genug und denke, es würde Überforderung und Enttäuschung eintreten. Die Nachbereitung soll neben einer emotionalen sowie fachlichen Auswertung der Exkursion auch einen Transfer beinhalten, der das Erlernte festigt.

Zur Differenzierung in der Lerngruppe, habe ich unter Berücksichtigung der in Kapitel 3.1 geschilderten Heterogenität Forschungsfragen mit Mindmap-Unterstützung vorgesehen sowie möglichst selbstdifferenzierende Aufgaben in Vor- und Nachbereitung entwickelt.

[Mathe-Unterricht] Vorbereitung der lokalen Änderungsrate

 Mathematik-Unterricht, Referendariat  No Responses »
Feb 212013
 

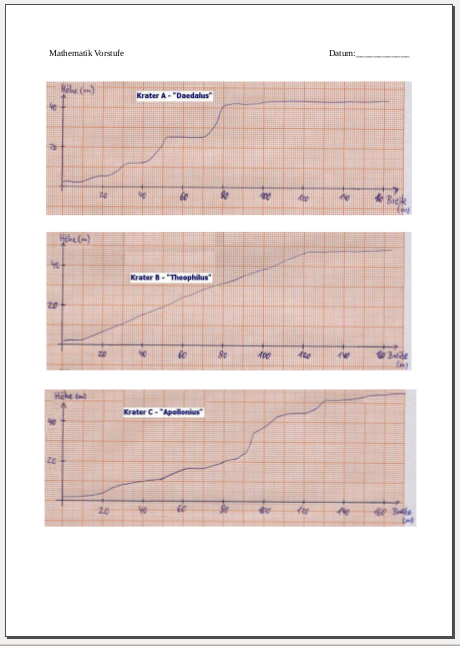
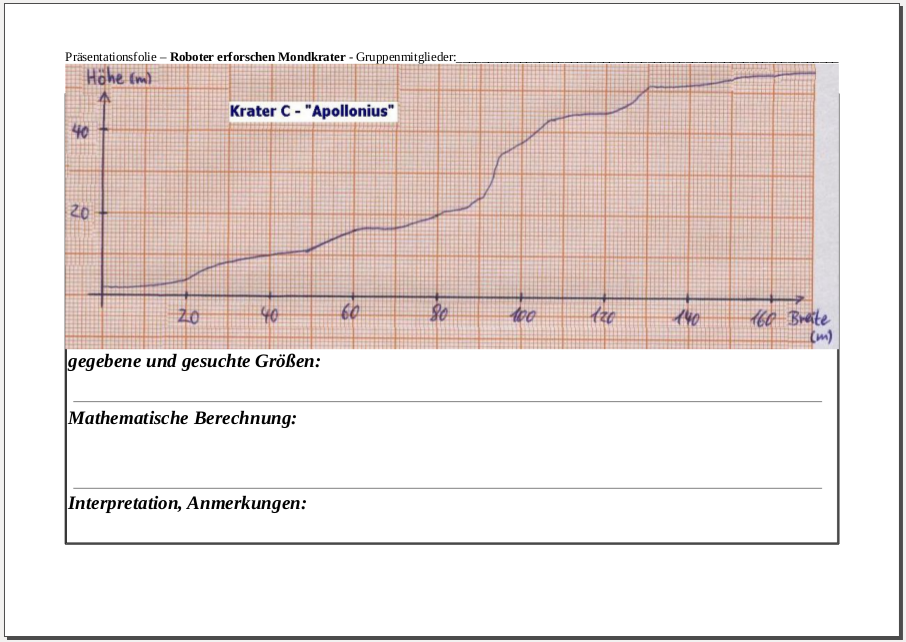
Als Gegenstand zur Vorbereitung der lokalen Änderungsrate habe ich gestern eine Stunde in der Vorstufe durchgeführt, die problemorientiert die Ermittlung von Steigungen auf verschieden großen Intervallen eines Graphen motivierte. Anhand eines aktuellen Zeitungsartikels zu geplanten Roboter-Einsätzen auf dem Mond, um in tiefen Kratern nach Wasser zu suchen wurde die Leitfrage aufgeworfen, welche Krater ein solcher Roboter mit einer gewissen Steigfähigkeit wieder verlassen kann. Anhand gegebener Graphen ermittelten die Schüler/innen zeichnerisch mehrere durchschnittliche Steigungen und präsentierten diese per Overhead-Folie. Trotz moderner Medien habe ich mich für die Arbeit mit solchen Folien entschieden, da sie während der Erarbeitung in Gruppen problemlos nebenbei gestaltet werden können. In der anschließenden Diskussion wurde thematisiert, wie eine maximale Steigung angenähert werden kann, um damit die lokale Änderungsrate als Ergebnis einer Grenzwert-Betrachtung immer kleinerer Intervalle zum Differenzenquotienten vorzubereiten. Abschließend wurde das Erlernte mit einem einfachen Lückentext und einer Hausaufgabe gesichert.

Als Aufhänger verwendete ich einen Zeitungsartikel zum Roboter-Einsatz auf dem Mond vom Handelsblatt. Das Deutsche Forschungszentrum für Künstliche Intelligenz (DFKI) forscht in Bremen seit Jahren an Robotern, die möglichst energiesparend und beweglich für Forschungen auf dem Mond eingesetzt werden sollen. Durch eine Impulsfrage von mir als Lehrer zu den Herausforderungen eines solchen Robotereinsatzes auf dem Mond sollten die Schüler/innen sich eigenständig der Leitfrage nähern, aber auch weitere wichtige Fragen im Kontext darstellen können.

Ich habe mich entschieden, den Schüler/innen drei Graphen zur Betrachtung zu geben, um einerseits motivierende Teilergebnisse zu sichern, da zwei der drei Graphen bereits sehr schnell eindeutige Aussagen zulassen. Der dritte Graph sollte dann analog zu den einfacheren ersten beiden bearbeitet werden und ist so konzipiert, dass er höhere Anforderungen mit sich brachte. In erster grober Näherung liegt die Steigung des dritten Kraters unter der Steigfähigkeit des Roboters, auf einigen kleinen Intervallen ist die Steigung dann aber über dieser, so dass er diesen Krater nicht verlassen kann. Somit wurde den Schüler/innen durch die Aufgabenstellung nahegelegt, kleinere Intervalle zu betrachten.

Arbeitsblatt Seite1

(Bildnachweise für das Arbeitsblatt: Roboter-Screenshot vom DFKI, Mondkrater unter public domain von der NASA)

Arbeitsblatt Seite2

(Bildnachweise: Eigene Produktion)

Eine der drei Präsentationsfolien

In der Nachbetrachtung hat sich das Problem des Roboter-Einsatzes als Unterrichtsgegenstand gelohnt, die Schüler/innen waren interessiert bei der Sache und die Leitfrage war einfach verständlich und damit der Arbeitsauftrag klar. Nach der Präsentation zielte ich mit einer Frage zur notwendigen, hypothetischen Steigfähigkeit eines Roboters zur Bewältigung eines gegebenen Kraters auf die Ermittlung der maximalen Steigung des Graphen. Diese kann nur als punktuelle Steigung sicher berechnet werden und somit wurde die Betrachtung lokaler Steigungen in den folgenden Stunden vorbereitend motiviert.

Materialien:

Arbeitsblatt-Gruppenarbeit (pdf)

Folie-A (pdf)

Folie-B (pdf)

Folie-C (pdf)

Arbeitsblatt-Lueckentext (pdf)

Arbeitsblatt-Hausaufgabe (pdf)

[Mathe-Unterricht] Darstellungsformen von Funktionen

 Mathematik-Unterricht  1 Response »
Feb 092013
 

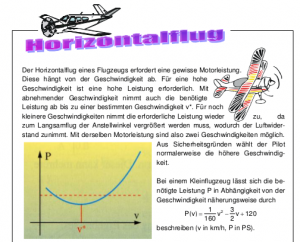
Als Vorbereitung auf den zentralen Begriff der Differentialrechnung, die Ableitung, habe ich die letzten Wochen im Mathematik-Unterricht der Vorstufe die Interpretation von Wertetabellen und Graphen geübt. Mit einer Aufgabe, die als Extremwertaufgabe mit der Ableitung direkt lösbar wäre, habe ich den Tiefpunkt per Wertetabelle und per grafischer Abschätzung bestimmen lassen. Die Aufgabe hierzu (Horizontalflug) habe ich von einem Kollegen empfohlen bekommen. Sie sind auch online erhältlich bei Frank Nordheim, der (seinen Schüler/innen) auch weitere Materialien zur Verfügung stellt.

ein Ausschnitt aus dem Material von Frank Nordheim

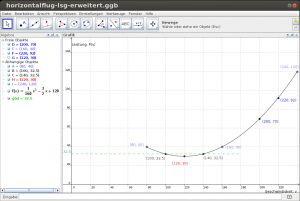
Die Aufgabe hierzu war, den Graphen zur Funktionsgleichung zu zeichnen, die Geschwindigkeiten zu einer gegebenen Leistung zu bestimmen sowie die Geschwindigkeit zur minimalen Leistung. Es gab Schwierigkeiten der Schüler/innen, zu erkennen, dass mit einer Ausnahme immer zwei Geschwindigkeiten zu einer Leistung gehören, da „wenn ich in die Formel nur eine Leistung einsetze ja auch nur eine Geschwindigkeit da steht“  Rechnerisch gehören bei einer quadratischen Funktion überwiegend zwei Lösungen zu einem Funktionswert, wobei scheinbar auch der Sachkontext verwirrte, in dem festgelegt war, dass für einen Flug mit sehr langsamer Geschwindigkeit ebenfalls höhere Leistung benötigt wird. Auch der Wechsel von einer „klassischen“ quadratischen Gleichung mit x und y als Variablen zu v und P(v) gestaltete sich als Hürde. Allerdings wurde in der Diskussion dann auch mit Hilfe einer geogebra-Visualisierung Klarheit geschaffen.

Eine Lösungsvariante zur Aufgabe

Im gleichen Kontext hatte ich vor, die Nützlichkeit von Tabellenkalkulations-Programmen zu zeigen, indem ich über eine Funktion, beispielsweise in Libre Office Calc Werte in immer kleineren Intervallen schachteln lasse. Hierzu bin ich zeitlich leider nicht mehr gekommen.

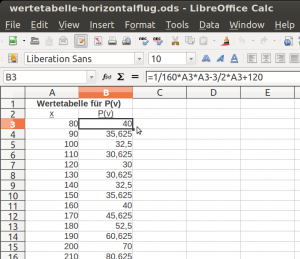
In einer Tabellenkalkulation lässt sich ein Extremwert durch Intervallschachtelung annähern, ohne eine Grafik erstellen zu müssen.

Zusätzlich habe ich als Wiederholung die beiden Punkte zur gegebenen Leistung von 32,5 Ps mit Hilfe der Funktionsgleichung und der quadratischen Ergänzung lösen lassen:

P(v) = 32,5 Ps = 1/160 v^2 – 3/2 v + 120

v^2 – 240 v + 14000 = 0

usw.

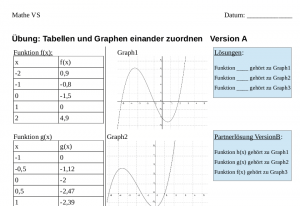
Als Sicherung habe ich zwei Versionen eines Arbeitsblattes ausgegeben, das jeweils die Lösung auf der anderen Version vorgegeben hat, um die Vernetzung der Darstellungsformen Wertetabelle und Graph zu stärken.

Ausschnitt des Arbeitsblattes Version A

Hier sind die Materialien zum weiterverwenden: Material-Darstellung-Tabelle-Graph.zip

[Mathe Unterricht] „Wieviele Maschinenteile lassen sich fertigen?“ – ein Anwendungskontext für Lineare Gleichungssysteme

 Mathematik-Unterricht, Referendariat  No Responses »
Jan 172013
 

Diese Woche habe ich eine Hospitationsstunde in der 11.Klasse recht erfolgreich umgesetzt.

Gegenstand der Stunde war ein Text aus dem Bereich meiner Ausbildung. Hierzu hatte ich einleitend einige Folien zum Problemlösen mit Mathematik und zu meiner Ausbildungsstätte, dem DESY (Deutsches Elektronen Synchrotron) und dem Arbeiten an mechanischen Fertigungsmaschinen im Unterrichtsgespräch eingebracht. Leider kann ich die verwendeten Fotos aus Lizenzgründen nicht auf meinem Blog veröffentlichen, aber bei der Eingabe von DESY in Suchmaschinen lassen sich auch so viele interessante Bilder finden.

Anschließend an die Problematisierung verteilte ich Arbeitsblätter in die Kleingruppen und gab den Auftrag, eine Präsentationsfolie vorzubereiten. Dies hatte gegenüber dem Smartboard oder Postern den Vorteil, dass sie zügig beschriftet werden kann und in der Gruppe am Tisch direkt zur Verfügung steht. Es gibt doch immer wieder auch gute Gründe, nicht die modernste, sondern die passendste Technik einzusetzen.

Hier ist die Aufgabenstellung, die zentral für die Stunde war:

Planung der Produktion von Maschinenbauteilen
In einer Firma, die Maschinenteile herstellt gibt es eine Bandsäge, eine Fräsmaschine und eine Drehbank.
Die Bandsäge steht aus betriebsinternen Gründen 9000 Minuten pro Woche zur Verfügung,
die Fräsmaschine 5200 Minuten und die Drehbank 5100 Minuten.
Es sollen drei Maschinenteile hergestellt werden (eine Kegel, ein Flansch und eine Welle).
Der Kegel benötigt 2 Minuten an der Bandsäge, 4 Minuten an der Fräsmaschine und 7 Minuten an
der Drehbank je Stück. Der Flansch benötigt 8 Minuten an der Bandsäge, 6 Minuten an der
Fräsmaschine und keine Zeit an der Drehbank je Stück. Die Welle benötigt 6 Minuten an der
Bandsäge, 1 Minute an der Fräsmaschine und 2 Minuten an der Drehbank je Stück.

Aufgabe:
Berechne die Anzahl der Maschinenteile, die in einer Woche hergestellt werden können,
so dass alle drei Maschinen optimal ausgelastet sind.

Der Text war bewusst komplex gestaltet, um das Strukturieren und mathematisieren von Informationen zu fördern. Dies gelang insgesamt auch recht gut. Die Gelenkstelle zwischen Problematisierung und Erarbeitung hatte ich etwas ungeschickt gestaltet und den Austausch über die Ergebnisse konnte nur angerissen werden abe ansonsten war die Stunde sehr erfolgreich. Die Gruppen entwurfen verschiedene Modell und verwarfen sie teilweise wieder, wie es bei Modellierungsaufgaben typisch ist. Die Sicherung holte ich die anschließende Stunde nach, so dass das Thema abgerundet werden konnte. Besonders zur Sinnstiftung halte ich die Aufgabe für günstig, da Lineare Gleichungssysteme meinen Schüler/innen bisher eher als reines Kalkül begegnet sind und sich im Alltag kaum Anwendungen erschließen.

Spannend war auch, dass eine Gruppe auf eine sehr ungewöhnliche Lösung gekommen war, die auch solide Ergebnisse ergab: Sie gingen schrittweise vor, indem sie erst eine Maschine möglichst effektiv mit zwei Bauteilen auslasteten, um die übrig gebliebene Zeit mit dem dritten Bauteil aufzufüllen. Eine Probier-Methode, die die Einsicht ermöglichte, dass unterschiedliche Strategien zum Ziel führen können.

Hier ist das für die Veröffentlichung gekürzte Material inklusive Stundenentwurf: UE Planung Maschinenbau

Diskussion zu Mathematikunterricht unter transkulturellen Gesichtspunkten

 Allgemein, Mathematik-Unterricht, Referendariat, Schule allgemein  2 Responses »
Okt 092012
 

In einer Fortbildung des Landesinstituts für Lehrerbildung in Hamburg zum Thema „interkulturelle Bildung“ haben wir uns an zwei Terminen mit verschiedenen Begriffen von „Kultur“ und Identitäten sowie der Sensibilisierung für einen transkulturellen Perspektivwechsel auseinandergesetzt.

Nach einer allgemeinen fachübergreifenden Einführung zu Identitäten und dem Umgang von Schule mit „Deutsch als Zweitsprache (DaZ)“ Schüler/innen beschäftigten wir uns handlungsorientiert mit Reaktionsmechanismen auf verschiedene „Regel“, um einen Umgang mit ungewohnten Verhaltensweisen durch eine sensibilisierte Sichtweise nachzuempfinden. Hierfür hatten wir ein Kartenspiel nach verschiedenen Regeln an verschiedenen Tischen gespielt ohne die Regeln explizit zu machen. Die Inhalte und Methoden bewegten den Blick weg vom „Problem mit den Schülern“ hin zum eigenen wertschätzenden Umgang mit „Fremdsein“ und dass nicht ohne Weiteres von sich auf andere geschlossen werden kann. Verschiedene Begrifflichkeiten und damit einhergehend Wertungen zu „Kultur“ wurden thematisiert und die Gespräche machten mir noch einmal deutlich, dass Erfahrungen mit „Fremdsein“ einigen Lehrer/innen durchaus fremd ist und wir als Lehrer/innen überwiegend weiß und bürgerlich mit Deutsch als erster Sprache behütet an Gymnasien sozialisiert wurden und somit systematisches Konfliktpotential in Schulen auftauchen muss. Dies einhergehend mit anderen gesellschaftlichen Rollen wie Gender, soziale Herkunft / Klasse und anderen Fremd- und Eigen-Identitätszuschreibungen erzeugt ein sehr komplexes Bild von sozialen Beziehungen in und um Schule.

Interessant fand ich bei der Beschäftigung mit den fachspezifischen didaktischen Überlegungen mit „transkultureller Brille“ (denn schließlich geht es weniger um Interkulturalität, also zwischen Kulturen arbeiten, sondern um die Einübung einer kulturübergreifenden und flexiblen Sichtweise auf kulturelle Praxen) die geringe Ausprägung dieser Sichtweise im Fach Mathematik. Sicherlich scheint Sprachunterricht zunächst naheliegender für eine transkulturelle Sichtweise zu sein, da Sprachförderung zur „Problembehebung“ mit DaZ Schüler/innen allgemein zum Standardprogramm gehört. Auf der anderen Seite erscheint gerade die Formalität und Fachsprache im Mathematik-Unterricht gerade für diese Schüler/inne mit DaZ eine Hürde darzustellen, die auf den Mangel an transkultureller Sichtweise in diesem Feld zurückzuführen ist. Wie in anderen Fächern auch gibt es eine doppelte Herausforderung für diese Schüler/innen, die Fachliche und die Sprachliche. Die Frage, die sich stellt, ist ob diesen Schüler/innen mit mehr Textarbeit und Sprachübungen im Mathematik-Unterricht geholfen ist oder mit bewusster Reduzierung der Fachsprache, um motivierende Erfolgserlebnisse zumindest auf mathematischer Ebenen zu ermöglichen. Ich denke wie häufig im pädagogischen Bereich gibt es nicht eine Antwort, sondern ein mehr oder weniger angemessenes Mischungsverhältnis. Insbesondere ist hierbei wichtig, die Unterrichtsvorbereitung und -nachbereitung immer wieder auch einmal durch eine „transkulturelle Brille“ zu reflektieren.

In unserer Kleingruppen-Arbeit zu Mathematik und transkultureller Bildung diskutierten wir eher über Zugänge zu mathematischen Konzepten allgemein, auch weil wir uns vorher in dieser Konstellation noch nie über didaktische Fragestellungen ausgetauscht hatten. Eines unserer Themen war: „Minus mal Minus gibt Plus“, wie kann das in den Horizont der Kinder gerückt werden? Ein weiteres Thema waren tragfähige Grundvorstellungen und Zugänge zu mathematischen Konzepten über verschiedene Strukturen wie grafische und ikonische Darstellungen und Arbeitsformen. Es wurde in Bezug auf andere Kulturkreise diskutiert, inwieweit Teamgeist und Kooperation in Kleingruppenarbeit stärker ausgeprägt seien und dies für den Unterricht nutzbar sei. Dann diskutierten wir über Aktivierung und Rollen in Gruppenarbeitsphasen sowie Anreize durch positive Verstärkung. Abschließend sprachen wir über Sprache und Mathematik-Unterricht. Mit einer transkulturellen Sichtweise kann in zwei Richtungen argumentiert werden, entweder die verstärkte Verwendung einfacher Sprache im Mathematikunterricht, um das Sprechen über Mathematik zu fördern und zu erleichtern oder entgegengesetzt die Verwendung von Sprache allgemein zu reduzieren, um die Doppelbelastung im Lernprozess zu reduzieren und auf die mathematischen Konzepte zu fokussieren. Viele Schüler/innen mit Deutsch als Zweitsprache haben Schwierigkeiten mit Formulierungen von Aufgaben. Dies lässt sich nach meiner Erfahrung im Sinne einer inklusiven Sichtweise noch weiter verschärfen darauf, dass allgemein auch Schüler/innen mit Deutsch als erster Sprache, die sprachliche Schwierigkeiten haben gleiche Doppelbelastungen erfahren.

In der Fachliteratur finden sich teilweise interessante Ansätze, die gerade die (mathematische) Sprachförderung ins Zentrum stellen, so beispielsweise das Arbeitsbuch „DaZ im Fachunterricht: Mathematik – Statistik für Anfänger“ (1). Auf der anderen Seite finden sich auch Aufgabentypen und inhaltliche Ansätze, die nach erster Sicht eher auf eigene Rassismen und Sensibilisierungen hinterfragt werden sollten. Wenn in Themenheften zu Mathematik und Interkulturalität neben „Tonleitern der Weltkulturen“ und „Kalenderberechnungen“ nur „Intelligenzvergleiche“, „Über- und Unterentwicklung“ und „Kriminalitätsraten“ als Titel auftauchen, darf man sich Sorgen machen, selbst wenn die Themen kritisch aufbereitet werden (was ich nur bedingt beurteilen kann, da ich sie nicht vollständig gesichtet habe, zudem ist einer der Artikel 11 Jahre alt). Da stellt sich die Frage, was für ein Bild von anderen Kulturen in Deutschland vorherrscht. Vergleiche (3) und (4)
Sinnvoll finde ich die folgende inhaltliche Bestimmungen auf der abstrakteren Ebene: „Im Mathematikunterricht kann die Vielfalt kultureller Wurzeln der eigenen Rechenkultur veranschaulicht, die Zahlensymbolik als Ausdruck bestimmter Weltdeutung behandelt oder bei Beispielaufgaben kulturelle Vielfalt repräsentiert werden.“ (http://www.bildungsserver.de/Mathematik-3383.html)
Das Buch „Zahlenwelten“ (2) hat ein ähnliches Mischungsverhältnis von Inhalten, die aus heutiger Sicht eher problematisch bis kontraproduktiv wirken, als auch Ansätze, die ich gerne ausprobieren möchte. Mathematisch logische Spiele aus anderen Kulturkreisen wie Patolli im Unterricht zu verwenden hat eben einen solchen wertschätzenden Bezug zu anderen Kulturen. Andererseits wird auch angeregt, statistisch „Ausländer an unserer Schule“ zu erheben und Berechnungen zu Unterkünften für Flüchtlinge anzustellen, die sicher kritisch begleitet Einsichten ermöglichen in gesellschaftliche Problemfelder, aber ebenso verstanden werden können, wie oben bereits benannt, dass andere Kulturen oder Kinder mit DaZ immer im negativen Kontext erwähnt werden oder als „das Andere“ dargestellt werden, statt ins Zentrum zu rücken, dass es kein „normal“ und „anders“ gibt, sondern alle Menschen in gewissen Kontexten als „normal“ gelten und in anderen als „anders“.

Zu unterscheiden bleibt das „strukturelle Mitdenken“ von transkultureller Bildung, z.B. durch Sprachwahl und Darstellungsarten und „inhaltliche Wandlung“ z.B. in Form vom wertschätzendem Aufgreifen verschiedener kulturell-historischer Wurzeln der Mathematik als Thema im Unterricht oder auch problemorientierte Beispiele, die nicht auf Fragestellungen aus dem Deutschen oder Europäischen Raum begrenzt bleiben.
Zum ersten Ansatz ist folgende Betrachtung hilfreich: „Betrachtet man das Spektrum schulischer Fächer genauer, so stellt sich heraus, dass es in allen Fächern kulturelle und fachgeschichtliche Prämissen und Traditionen gibt, die sich bei einer „interkulturellen Revision“ – mal mehr, mal weniger – als sperrig erweisen.“ (3) Beim zweiten Ansatz ist immer auch die Hinterfragung der eigenen Position als wohlmöglich Weißer Europäer mit Deutsch als Erstsprache unabdingbar, ist doch schnell aus gutem Vorhaben ein schräges Bild geworden, in dem es nicht um eine transkulturell reflektierte selbstbestimmte Identität der Schüler/innen, sondern um Zuschreibungen mit einhergehenden Wertungen von außen geht. Hier sollte nach meiner Einschätzung die Schüler/innen-Zentrierung in der Methodik besonders stark gemacht werden.

Literatur zum Thema:

(1) Nina Bödeker Olaf Gent: „DaZ im Fachunterricht: Mathematik – Statistik für Anfänger“ 5./6. Klasse, Persen Verlag 2010 (http://buecher-de.welt.de/shop/deutsch-als-fremdsprache/mathematik-statistik-fuer-anfaenger/boedeker-nina-gent-olaf/products_products/detail/prod_id/30530497/)

(2) Joachim Schroeder: „Zahlen-Welten: Bausteine für einen interkulturellen Mathematikunterricht“ Armin Vaas Verlag, 1994 (http://www.buchpreis-suche.de/zahlen-welten-bausteine-f%C3%BCr-einen-interkulturellen-mathematikunterricht.htm)

(3) Mathematik-Unterrichts-Einheiten-Datei e.V. „interkulturelles Lernen„: http://www.mued.de/html/inhalte/i3-multikulti.html

(4) Handreichung: Impulse für das interkulturelle Lernen Forum 1 / 2001, UNESCO Projekt Schulen http://www.ups-schulen.de/forum/01-1/forum-27-37.pdf

(5) S.Prediger: „Mathematiklernen als interkulturelles Lernen – Entwurf für einen didaktischen Ansatz„, in: Journal für Mathematikdidaktik 22 (2001) (http://www.mathematik.uni-dortmund.de/~prediger/veroeff/01-jmd-ml-as-ik.html)

[Mathe Unterricht] „Passt der LKW durch den Tunnel?“ – quadratische Funktionen

 Allgemein, Mathematik-Unterricht, Referendariat  No Responses »
Sep 032012
 

Da ich mich gerade im Referendariat befinde, veröffentliche ich auch Teile meiner Auseinandersetzung mit der Ausbildung auf diesem Blog.

Vor einigen Tagen habe ich eine Hospitation in der Vorstufe (Klasse 11)  in Mathe durchgeführt und mich dabei unserem derzeitigen (Wiederholungs-)Unterrichtsgegenstand „quadratische Funktionen“ problemorientiert genähert. Gar nicht so einfach, wie ich finde, wo quadratische Funktionen im Alltag nicht so üblich zu finden sind wie geometrische oder stochastische Figuren und Konzepte.

Angelehnt an den schriftlichen Überprüfungen Mathematik (pdf) der Klasse 10 in Hamburg  habe ich mich dem Thema „Brückenbau“ genähert und eine gelungene Problemstellung gefunden, die sich in verschiedener Ausprägung häufiger auch im Netz findet (wenn bei google „brücke parabel lkw aufgabe“ eingegeben wird, erscheinen einige Treffer zu ähnlichen Aufgaben)

Die Problemstellung sollte allerdings durch einen stummen Impuls mit Bild von den Schüler/innen selbst gefunden werden, was auch relativ gut klappte, dann aber zu wenig im Unterrichtsgespräch fokussiert wurde.

„Wie hoch muss eine parabelförmige Brücke konstruiert werden, damit ein LKW gut hindurchpasst?“

Fachlich ist das Problem über die Auswahl einer günstig gestauchten Parabelform zu lösen, für die dann entsprechend ein Funktionswert zu gegebener Breite berechnet wird, der den Höhenabschnitt von LKW Oberseite zum Tunnel-Scheitelpunkt im Betrag ergibt. Eine hohe Hürde stellt die Modellierung dar, aber das mathematische Problem ist im Grunde genommen eine Wiederholung aus der Mittelstufe.

Ich veröffentliche hier auch meinen Unterrichtsentwurf in Teilen, personenbezogene Daten selbstverständlich nicht. Gerade in der Anzahl der Lernziele (viel zu Viele) und in der Genauigkeit der Verlaufsplanung könnte der Unterrichtsentwurf noch einmal kritisch überarbeitet werden. Bei einer offenen Problemstellung muss man auch immer damit rechnen, dass völlig andere als die intendierten Vorschläge zum Thema werden, beim hier eingesetzten Bild beispielsweise Geschwindigkeiten oder geometrische Aspekte. Dabei sollte das „Ostereierraten“ vermieden werden, indem auch nicht-intendierte Vorschläge entsprechend gewürdigt werden, aber das Thema der Unterrichtsstunde im Unterrichtsgespräch fokussiert werden. Ich habe mir auch vorgenommen, die Selbstreflexion anders aufzubauen, entweder mit abhak-Kästchen oder mit mehreren Abstufungen zum ankreuzen statt wie in diesem Material geplant mit offenen Feldern. Aber bei allen selbstkritischen Überlegungen, vielleicht hilft er ja der einen oder dem anderen beim Schreiben solcher Entwürfe oder beim Durchführen eines ähnlichen Unterrichtsbausteines.

Materialien:

UE-Morisse-28.08-fuer-blog.odt

Hilfekarten.pdf

zusätzliche-Problemstellungen.pdf

reflexion-mathe-vs.pdf

 Older Entries  Newer Entries